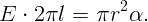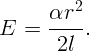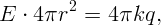
Найти напряженность поля и потенциал во всем пространстве тонкой сферы радиуса R, равномерно заряженной до заряда q.
Решение
Применим теорему Гаусса. Выберем в качестве замкнутой поверхности концентрическую сферу радиуса r > R (рис.). Очевидно, что напряженность на поверхности этой сферы будет одинакова по величине и направлена по радиусу. Тогда поток напряженности через нее будет E ⋅ 4πr2. Согласно теореме Гаусса
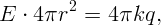
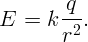
Выбрав в качестве поверхности сферу радиуса r < R, получим E = 0. Таким образом, однородно заряженная сфера во внешней области пространства создает такое же поле, как и заряд, помещенный в ее центре. Внутри сферы поля нет.
Найдем потенциал сферы во всем пространстве. Так как вне сферы напряженность поля совпадает с напряженностью заряда, находящегося в центре, то и потенциал при r > R выразится в виде
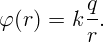
Пронесем единичный положительный заряд из бесконечности до расстояния r от центра, меньшего радиуса сферы. Тогда работа, которую необходимо совершить по переносу до поверхности сферы будет равна kq∕R. Внутри сферы поле равно нулю и работа не совершается. Таким образом
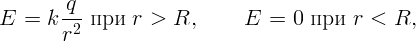

На рис. 3.1 изображены графики зависимости напряженности и потенциала поля от расстояния до центра однородно заряженной сферы.
Однородно заряженный шар. Пусть радиус шара R, полный заряд Q. Повторяя рассуждения, приведенные в предыдущей задаче, получим, что вне шара напряженность и потенциал поля совпадают с полем заряда Q, помещенного в центр шара:

Чтобы найти напряженность электрического поля внутри шара, выберем в качестве замкнутой поверхности сферу радиуса r < R с центром в центре шара. Из симметрии ясно, что напряженность поля направлена по радиусу и одинакова по величине на всей поверхности сферы. Из теоремы Гаусса следует
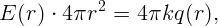
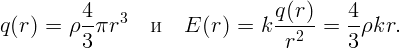
Плотность заряда равна полному заряду, деленному на объем шара:
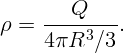
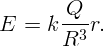
Найдем потенциал внутри шара.
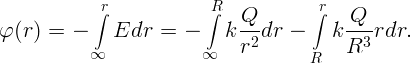
Первый интеграл имеет смысл работы по переносу единичного положительного заряда из бесконечности до поверхности шара и равен kQ∕R. Второй член
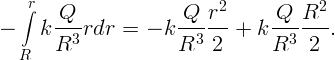
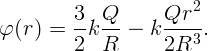
Окончательно имеем
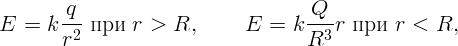
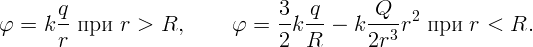
Пусть есть две проводящие концентрические сферы радиусов a и b. На внутреннюю сферу помещен заряд q, а внешняя заземлена (рис. 3.3). Требуется определить напряженность и потенциал электрического поля во всем пространстве.
Решение
Так как внешняя сфера заземлена, на ней появляется некоторый заряд Q. Если бы он был известен, напряженность поля легко определилась бы из принципа суперпозиции (напомним, что во внешнем пространстве сфера создает поле, такое же, как точечный заряд, расположенный в ее центре, а внутри поля нет)
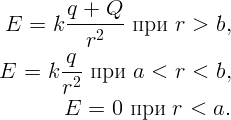
Для потенциала при r > b имеем φ = k(q + Q)∕r. На поверхности внешней сферы φ(b) = k(q + Q)∕b.
Так как эта сфера заземлена, φ(b) = 0. Отсюда
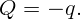
Тогда напряженность поля при r > b равна нулю. Вне заземленной сферы поля нет. Этот результат не зависит от формы заземленного проводника. Говорят, что заземленная оболочка экранирует находящиеся внутри заряды: никакие изменения их величины или положения не сказываются снаружи.
Понятно, что при r > b потенциал равен нулю. Для нахождения потенциала между сферами пронесем единичный положительный заряд из бесконечности в данную точку, используя принцип суперпозиции. В поле заряда Q работа совершается лишь до поверхности внешней сферы: φ1 = kQ∕b--kq∕b. А в поле внутренней сферы φ2 = kq∕r. Полный потенциал
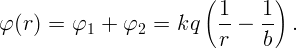
Внутри малой сферы E = 0, потенциал не меняется и равен потенциалу на поверхности
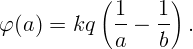
На рис. 3.4 приведены графики зависимостей E(r) и φ(r).
Четыре одинаковых частицы массы m и заряда q первоначально удерживаются в углах квадрата со стороной a. Заряды отпускают. Найти скорости зарядов по прошествии большого промежутка времени.
Решение
Из симметрии ясно, что в любой момент времени частицы будут находиться в углах некоторого квадрата и обладать одинаковыми по величине скоростями, направленными по диагоналям этого квадрата. В результате вся начальная потенциальная энергия U перейдет в кинетическую энергию частиц
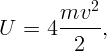
Дело, таким образом, сводится к вычислению начальной потенциальной энергии системы U. Перенумеруем заряды (рис. 3.5) и начнем «собирать» систему. Принесем из бесконечности первый заряд. Для этого не понадобиться совершать работу (внешних сил нет): A1 = 0.
Принесем второй заряд. Работа в поле первого заряда будет
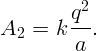
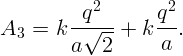
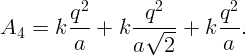
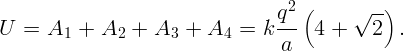
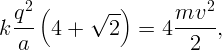
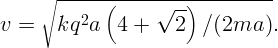
С большого расстояния навстречу друг другу со скоростями, соответственно, v1 и v2 движутся две одинаковых частицы массы m и заряда q. Определите минимальное расстояние, на которое они сблизятся.
Решение
При минимальном расстоянии скорости частиц u будут одинаковы. Из закона сохранения импульса
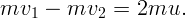
Запишем закон сохранения энергии:
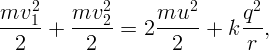
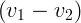 ∕2. И,
подставляя во второе, получаем ответ:
∕2. И,
подставляя во второе, получаем ответ:
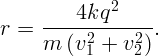
Определите емкость системы конденсаторов, изображенных на рисунке (рис. 3.6).
Решение
Пронумеруем конденсаторы и обозначим на схеме заряды (рис. 3.7). Из симметрии схемы ясно, что заряды на конденсаторах 1, 2 и 3, 4, соответственно, одинаковы. Так как батарея электронейтральна q1 = q2.
Тогда ясно, что средний (5-й) конденсатор не заряжен и его можно убрать. Эквивалентная схема будет выглядеть так: (рис 3.8).
Так как емкость последовательно соединенных конденсаторов определяется по формуле
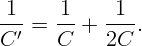
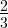 C. И имеем новую эквивалентную схему (рис. 3.9). По правилу
определения емкости параллельно соединенных конденсаторов полная емкость
цепи:
C. И имеем новую эквивалентную схему (рис. 3.9). По правилу
определения емкости параллельно соединенных конденсаторов полная емкость
цепи:
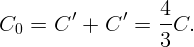
Можно было поступить иначе. Так как средний конденсатор не заряжен, точки, к которым он подсоединен, имеют одинаковый потенциал. Тогда их можно соединить проводником: это не приведет к перераспределению зарядов на остальных конденсаторах. Соответствующая эквивалентная схема (рис. 3.10. Или, учитывая, что имеется две пары параллельно соединенных конденсаторов, получаем еще одну эквивалентную схему (рис. 3.11). Отсюда
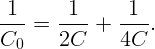
В итоге получаем тот же ответ:
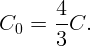
Каким должно быть сопротивление r, чтобы входное сопротивление между клеммами было равно тоже r (рис. 3.12)?
Решение
Последние два сопротивления, соединенные последовательно, имеют сопротивление
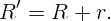
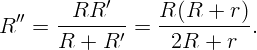
То есть:
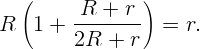
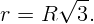
Батарея, замкнутая на сопротивление R1 = 10 Ом, дает ток I1 = 3 А; замкнутая на сопротивление R2 = 20 Ом, она дает ток I2 = 1,6 А. Найдите ЭДС и внутреннее сопротивление r батареи.
Решение
Из условия

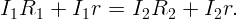
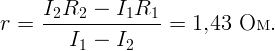
Подставляя r в первое уравнение, получим
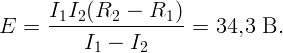
Аккумулятор подключен один раз к внешней цепи с сопротивлением R1, другой раз – с R2. При этом количество теплоты, выделяющейся во внешней цепи в единицу времени, одинаково. Определите внутреннее сопротивление аккумулятора.
Решение
Обозначим ЭДС аккумулятора через , а внутреннее сопротивление – через r.

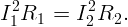
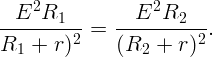
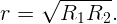
Конденсаторы емкости C1 и C2 и резисторы, сопротивления которых равны R1,R2,R3, включены в электрическую цепь, как показано на рисунке 3.15). Найти установившиеся заряды на конденсаторах. Напряжение U известно.
Решение
В установившемся режиме через резисторы течет постоянный ток, определяющийся из уравнения
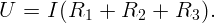
Рассмотрим контур, содержащий C1,R1,R2. Для него:
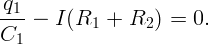
Откуда (подставляя I):
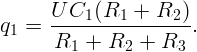
Аналогично, рассматривая контур, содержащий C2,R2,R3, получим
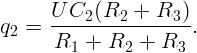
На заряд q = 1 Кл, движущийся со скоростью v = 1 м/с, в магнитном поле действует сила F = 10 Н. Заряд движется под углом α = 30∘ к направлению индукции магнитного поля. Чему равна индукция этого поля?
Решение
На заряд действует сила Лоренца:
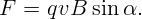
Откуда B = F∕(qv sin α). Подставляя числа, получим ответ: B = 20 Тл.
В вертикальном однородном магнитном поле на двух тонких нитях подвешен горизонтально проводник массы m = 0,16 кг и длины l = 0,8 м. Концы проводника при помощи гибких проводов, находящихся вне поля, подсоединены к источнику тока. Найдите угол, на который отклоняются от вертикали нити подвеса, если по проводнику течет ток I = 2 А, а индукция магнитного поля B = 1 Тл.
Решение
На проводник действуют две силы: тяжести mg, направленная вертикально, и Ампера IBl, направленная горизонтально (см. рис. 3.16). Тогда в равновесии
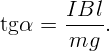
Как относятся радиусы траекторий двух электронов с кинетической энергией K1 и K2, если однородное магнитное поле перпендикулярно их скорости?
Решение
Скорости электронов определяются из формул:
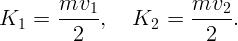
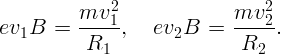
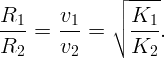
В однородном магнитном поле индукции B находятся две вертикальные рейки, расположенные в плоскости, перпендикулярной линиям поля (рис. 3.17). По рейкам, расстояние между которыми равно L, может скользить без трения проводник массой m. Определите установившуюся скорость этого проводника, если верхние концы реек замкнуты на сопротивление R. В какие виды энергии переходит работа силы тяжести?
Решение
На скользящий проводник действуют две силы: тяжести mg и Ампера IBL. При установившемся движении
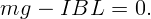
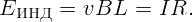
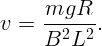
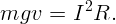
Металлический стержень AB, сопротивление единицы длины которого ρ, движется с постоянной скоростью v, перпендикулярной AB, замыкая два идеальных проводника OC и OD, образующих друг с другом угол α. Длина OC равна l, и AB перпендикулярен OC (рис. 3.18). Вся система находится в однородном постоянном магнитном поле индукции B, перпендикулярном плоскости системы. Найдите полное количество теплоты, которое выделится в цепи за время движения стержня от точки O до точки C.
Решение
Площадь треугольника в зависимости от времени S = xy∕2, где x = vt,y = x ⋅ tgα = vt ⋅ tgα.
Тогда
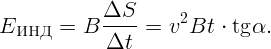
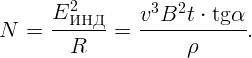
Тогда ответ
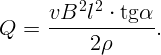
Индукция однородного магнитного поля внутри цилиндра радиуса r = 0,1 м линейно возрастает со временем: B = αt (коэффициент α = 10-3 Тл/с). Магнитное поле направлено вдоль оси цилиндра. Чему равна напряженность вихревого электрического поля на расстоянии l = 0,2 м от оси цилиндра?
Решение
Циркуляция электрического поля равна скорости изменения магнитного потока через сечение цилиндра: