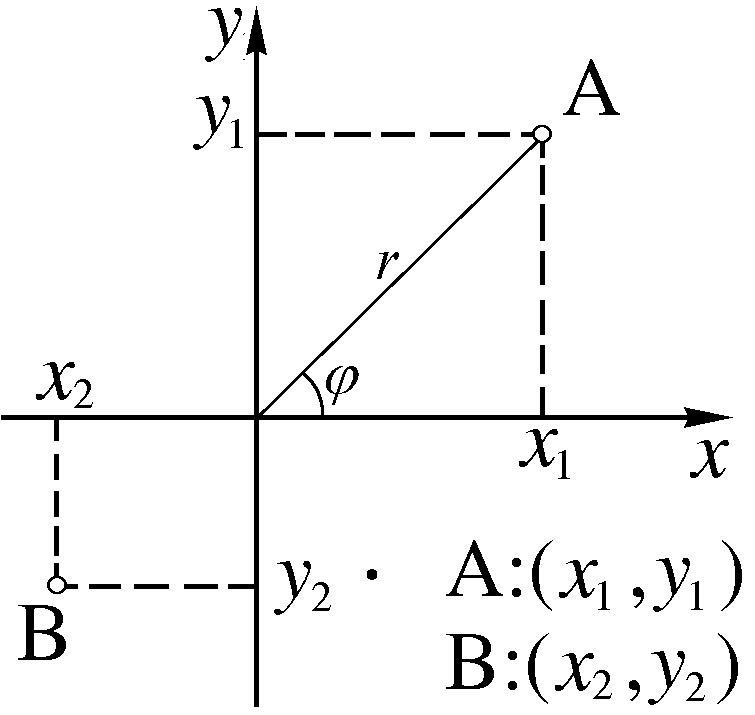
|
Основная единица времени – секунда. В эталонных часах, использующих излучение атомов цезия, секунда определяется как 9192631770 периодов колебаний излучения. Предыдущее астрономическое определение секунды (1/86400 доля суток) очень близко к современному, но неудобно для использования, так как длительность суток изменяется из-за неравномерности вращения Земли. Сейчас дважды в год астрономическое время корректируется по атомным часам: добавляется недостающая или вычитается лишняя секунда.
На Генеральной конференции мер и весов в 1983 году метр определен как расстояние, которое свет проходит за 1/299792458 долю секунды. В пределах точности это определение совпадает с более ранним (эталонная "линейка").
Чтобы описать движение, нужно указывать положение тел. Проще всего это сделать для тел малых размеров. Тела, размерами которых при описании движения можно пренебречь, называют материальными точками.
Для указания положения и описания движения тел и частиц специально выбирают одно из тел. Его называют телом отсчета. Все измерения проводятся от выбранного тела отсчета.
Декартовы координаты. На плоскости из выбранного начала
отсчета O проводятся под прямым углом две координатные оси X и Y
(рис. 1.1). Из интересующей нас точки опускаются перпендикуляры
на оси и прочитываются на них координаты 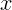 и
и 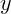 . Координаты
точки принято записывать в круглых скобках числами через запятую:
. Координаты
точки принято записывать в круглых скобках числами через запятую:
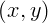 .
.
Расстояние 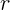 от начала отсчета до частицы определяется из теоремы
Пифагора:
от начала отсчета до частицы определяется из теоремы
Пифагора:
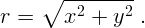
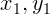 ) и (
) и (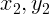 ) расстояние между
ними
) расстояние между
ними
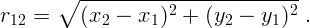
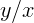 дает тангенс угла, под которым видна точка из
начала отсчета O по отношению к оси X (рис. 1.1):
дает тангенс угла, под которым видна точка из
начала отсчета O по отношению к оси X (рис. 1.1):
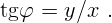
Числа 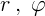 – это полярные координаты точки. В физике удобнее
работать с углами не в градусной, а в радианной мере. Из вершины угла
описывают окружность и задают величину угла отношением длины отсекаемой
дуги к радиусу (рис. 1.2):
– это полярные координаты точки. В физике удобнее
работать с углами не в градусной, а в радианной мере. Из вершины угла
описывают окружность и задают величину угла отношением длины отсекаемой
дуги к радиусу (рис. 1.2):
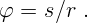
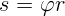 .
.
В пространстве из начала отсчета выходят три взаимно перпендикулярных
координатных оси X, Y и Z. Через точку проводятся три плоскости,
перпендикулярные осям. Их пересечения с осями и задают координаты частицы
(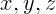 ).
).
Расстояние от начала координат до выбранной точки дается выражением
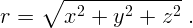
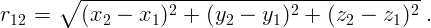
Положение точки можно задать и направленным отрезком (вектором).
Радиус-вектор частицы проводится из начала координат в точку M, где
находится частица. Радиус-вектор 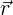 указывает, в каком направлении и на
каком расстоянии от начала отсчета находится точка. Векторы при записи
выделяются стрелкой сверху или черточкой (в книгах – жирным шрифтом:
указывает, в каком направлении и на
каком расстоянии от начала отсчета находится точка. Векторы при записи
выделяются стрелкой сверху или черточкой (в книгах – жирным шрифтом:
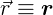 ).
).
Если частица перешла из точки A в точку B, то изменение ее положения
называется перемещением и описывается направленным отрезком 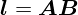 (рис. 1.3). Частица не обязательно двигалась от A к B по прямой. При любых
промежуточных этапах перемещение от начальной точки A до конечной точки
B однозначно задается вектором
(рис. 1.3). Частица не обязательно двигалась от A к B по прямой. При любых
промежуточных этапах перемещение от начальной точки A до конечной точки
B однозначно задается вектором 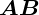 .
.
Результат последовательных перемещений, переводящих частицу из точки A в точку B, а затем в точку C, таков же, как и одного перемещения из точки A сразу в C. Значит, векторы перемещения можно складывать:
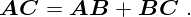
Чтобы сложить два вектора, в конец первого слагаемого 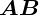 переносим
начало второго слагаемого
переносим
начало второго слагаемого 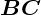 . Замыкающая стрелка от начала первого к
концу второго вектора дает сумму
. Замыкающая стрелка от начала первого к
концу второго вектора дает сумму 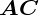 . Такое правило сложения векторов
называется правилом треугольника. Складывать можно не только
перемещения, но и любые другие векторы (скорости, силы...) Правило сложения
обобщается на случай любого числа слагаемых: они выстраиваются в ломаную
линию, каждое последующее слагаемое откладывается от конца предыдущего.
Вектор, проведенный из начала в конец этой ломаной линии, дает сумму (рис.
1.4).
. Такое правило сложения векторов
называется правилом треугольника. Складывать можно не только
перемещения, но и любые другие векторы (скорости, силы...) Правило сложения
обобщается на случай любого числа слагаемых: они выстраиваются в ломаную
линию, каждое последующее слагаемое откладывается от конца предыдущего.
Вектор, проведенный из начала в конец этой ломаной линии, дает сумму (рис.
1.4).
Вектор 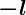 противоположен по направлению вектору
противоположен по направлению вектору 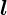 . Разность
векторов
. Разность
векторов 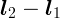 определяется как сумма
определяется как сумма 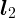 и
и 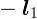 :
:
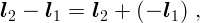
Простейшее движение – вдоль прямой. При этом изменяется координата тела
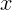 в зависимости от времени
в зависимости от времени 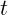 , что записывается кратко в виде:
, что записывается кратко в виде:
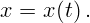
Средней скоростью на промежутке времени от 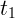 до
до 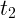 называется
отношение перемещения к интервалу времени:
называется
отношение перемещения к интервалу времени:
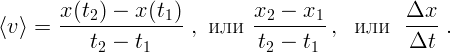 | (1.1) |
При стремлении интервала времени и перемещения к нулю в пределе получается мгновенная скорость:
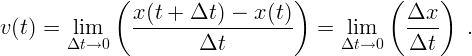 | (1.2) |
Здесь 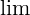 обозначает предел (сокращенное limit) выражения в скобках при
обозначает предел (сокращенное limit) выражения в скобках при
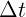 , стремящемся к нулю.
, стремящемся к нулю.
Более компактно мгновенную скорость принято записывать так:
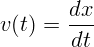 | (1.3) |
Обозначения 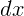 и
и 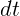 можно понимать как бесконечно малые
изменения координаты и времени. Операция (1.3), или, что то же, (1.2),
называется вычислением производной
можно понимать как бесконечно малые
изменения координаты и времени. Операция (1.3), или, что то же, (1.2),
называется вычислением производной 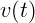 для функции
для функции 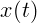 , или
дифференцированием координаты по времени. Малые приращения
, или
дифференцированием координаты по времени. Малые приращения
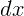 и
и 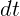 называют дифференциалами (от иностранного слова
difference).
называют дифференциалами (от иностранного слова
difference).
Ускорение – это скорость изменения скорости:
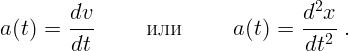 | (1.4) |
От координаты получается вторая производная (производная от производной).
Пусть 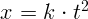 , где
, где 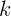 – постоянный коэффициент. Тогда, опуская знак
предела везде, кроме последнего равенства, получим
– постоянный коэффициент. Тогда, опуская знак
предела везде, кроме последнего равенства, получим
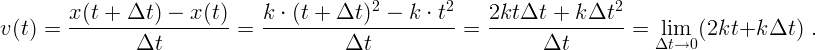
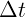 к нулю:
к нулю:
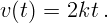
Выражение уже не содержит никакого интервала и зависит только от одного
времени 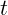 . Это и есть мгновенная скорость для данной зависимости
. Это и есть мгновенная скорость для данной зависимости 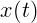 .
Заметим, что сначала надо вычислить и по возможности упростить выражение,
а уж потом переходить к пределу. Если, наоборот, сразу положить
.
Заметим, что сначала надо вычислить и по возможности упростить выражение,
а уж потом переходить к пределу. Если, наоборот, сразу положить 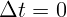 ,
получится неопределенность 0/0.
,
получится неопределенность 0/0.
Ускорение в этом примере
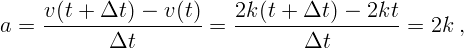
то есть постоянно.
Производная от постоянной величины равна нулю: 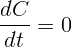 .
.
Производная суммы функций равна сумме производных: 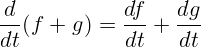 .
.
Производная произведения: 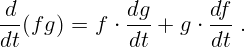
В частности, для произведения функции на постоянную величину
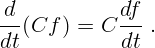
Производная частного: 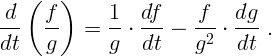
Производная сложной функции: 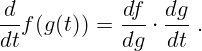
Производные от наиболее важных функций (величины 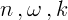 постоянны):
постоянны):
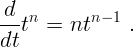
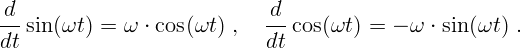
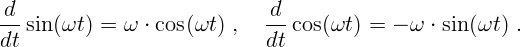
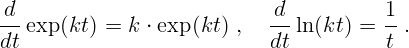
Пользуясь таблицей и правилами дифференцирования, можно найти производные от любой комбинации указанных функций.
На рисунке 1.5 приведен график зависимости положения частицы от
времени, то есть график функции 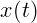 . Он гораздо нагляднее, чем таблица
или формула.
. Он гораздо нагляднее, чем таблица
или формула.
Видно, например, что на интервале времени от 1 до 3,5 с координата растет.
Значит, в течение этого промежутка частица удаляется от начала координат.
Затем виден участок (3,5 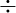 6 с), на котором координата постоянна. Значит, на
некоторое время частица остановилась. Уменьшение координаты (участок 6
6 с), на котором координата постоянна. Значит, на
некоторое время частица остановилась. Уменьшение координаты (участок 6 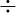 7 с) означает, что частица двинулась назад.
7 с) означает, что частица двинулась назад.
Геометрически мгновенная скорость – это тангенс угла между касательной
к непрерывной кривой 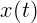 и осью
и осью 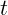 . Короче можно говорить просто
«наклон» вместо «тангенс угла наклона касательной».
. Короче можно говорить просто
«наклон» вместо «тангенс угла наклона касательной».
В момент времени 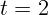 с к графику проведена касательная. Измерив катеты
треугольника, изображенного на рисунке, получаем
с к графику проведена касательная. Измерив катеты
треугольника, изображенного на рисунке, получаем 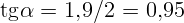 м/с.
м/с.
Совершенно так же по графику скорости 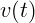 находится ускорение.
Наклон касательной к графику скорости – это и есть ускорение в данный
момент времени.
находится ускорение.
Наклон касательной к графику скорости – это и есть ускорение в данный
момент времени.
Траектория есть линия, описываемая частицей при движении в пространстве.
Ускорение частицы при движении по кривой траектории можно разложить на
две взаимно перпендикулярные компоненты: центростремительное
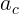 (перпендикулярное вектору скорости
(перпендикулярное вектору скорости 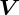 ) и тангенциальное
) и тангенциальное 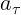 (параллельное скорости, и, значит, траектории в данной точке). Выполняются
равенства
(параллельное скорости, и, значит, траектории в данной точке). Выполняются
равенства
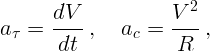
где 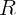 – радиус кривизны траектории в данной точке.
– радиус кривизны траектории в данной точке.
Определим радиус кривизны траектории тела, брошенного под углом 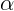 к
горизонту, в верхней и начальной точках. В верхней точке траектории
скорость равна
к
горизонту, в верхней и начальной точках. В верхней точке траектории
скорость равна 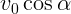 и направлена горизонтально (вертикальная
составляющая скорости обращается в нуль). Ускорение
и направлена горизонтально (вертикальная
составляющая скорости обращается в нуль). Ускорение 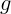 перпендикулярно
скорости, то есть в этой точке все ускорение – чисто центростремительное.
Тогда можно записать:
перпендикулярно
скорости, то есть в этой точке все ускорение – чисто центростремительное.
Тогда можно записать: 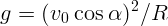 , откуда радиус кривизны
траектории:
, откуда радиус кривизны
траектории:
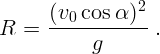
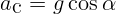 , а скорость равна
, а скорость равна 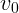 . Имеем:
. Имеем:
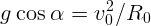 , и радиус кривизны
, и радиус кривизны
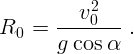
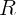 , то есть траектория в начальной точке менее
«кривая». Тангенциальное ускорение в начальной точке
, то есть траектория в начальной точке менее
«кривая». Тангенциальное ускорение в начальной точке 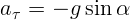 . Оно
отрицательно, то есть величина скорости в этот момент уменьшается.
. Оно
отрицательно, то есть величина скорости в этот момент уменьшается.
Между физическими телами существуют взаимодействия, количественно характеризуемые силами.
Первый закон Ньютона: в инерциальной системе отсчета тело, на которое нет внешних воздействий, движется равномерно и прямолинейно (в частности, может и покоиться).
Второй закон Ньютона:
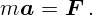
Здесь 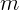 – масса тела,
– масса тела, 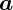 – его ускорение,
– его ускорение, 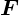 – векторная сумма сил,
действующих на тело.
– векторная сумма сил,
действующих на тело.
Третий закон Ньютона: при взаимодействии двух тел (допустим, 1 и 2) силы их взаимодействия противоположны,
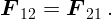
Второй и третий законы Ньютона позволяют определять действующие силы по известному движению. Так были найдены силы тяготения, упругости, трения и пр. Полученные закономерности применяют для определения движения тел в новых условиях.
Пусть бруски масс 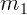 и
и 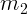 соприкасаются, и первый брусок толкают с
заданной силой
соприкасаются, и первый брусок толкают с
заданной силой 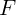 (рис. 1.6).
(рис. 1.6).
Тела, как известно из опыта, могут двигаться вместе, сохраняя
соприкосновение. Для такого движения найдем ускорение 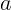 , одинаковое для
обоих тел. Из второго закона Ньютона
, одинаковое для
обоих тел. Из второго закона Ньютона
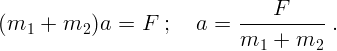
На тело 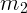 действует пока неизвестная сила
действует пока неизвестная сила 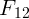 со стороны первого.
Записываем второй закон Ньютона:
со стороны первого.
Записываем второй закон Ньютона:
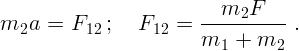
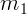 действует известная сила
действует известная сила 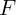 и сила со стороны второго тела
и сила со стороны второго тела 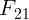 .
Значит, равнодействующая сил, приложенных к
.
Значит, равнодействующая сил, приложенных к 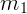 , равна
, равна 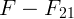 .
Тогда
.
Тогда
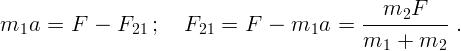
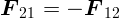 . Видим, что это равенство
выполняется: силы
. Видим, что это равенство
выполняется: силы 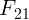 и
и 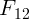 одинаковы по величине и направлены в
противоположные стороны (см. рис. 1.6). При этом совершенно не существенно,
как взаимодействуют тела (сколько точек соприкосновения, каковы упругие
свойства материалов и т.д.). Все, что нам понадобилось – второй и третий
законы Ньютона и тот опытный факт, что тела могут ускоряться вместе,
сохраняя соприкосновение. Тела могли бы быть склеены или вообще быть
частями единого тела.
одинаковы по величине и направлены в
противоположные стороны (см. рис. 1.6). При этом совершенно не существенно,
как взаимодействуют тела (сколько точек соприкосновения, каковы упругие
свойства материалов и т.д.). Все, что нам понадобилось – второй и третий
законы Ньютона и тот опытный факт, что тела могут ускоряться вместе,
сохраняя соприкосновение. Тела могли бы быть склеены или вообще быть
частями единого тела.
Рассмотрим движение по окружности, когда известно центростремительное
ускорение тела. Пусть автомобиль с массой 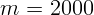 кг проезжает по
выпуклому мосту, имеющему радиус кривизны
кг проезжает по
выпуклому мосту, имеющему радиус кривизны 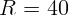 м, со скоростью
м, со скоростью
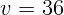 км/час (10 м/с). С какой силой автомобиль давит на мост в его
середине?
км/час (10 м/с). С какой силой автомобиль давит на мост в его
середине?
Центростремительное ускорение 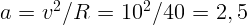 м/с
м/с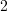 . Вектор
ускорения направлен вниз. На автомобиль действует сила тяжести
. Вектор
ускорения направлен вниз. На автомобиль действует сила тяжести 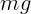 и
сила со стороны моста (сила реакции)
и
сила со стороны моста (сила реакции) 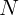 . Из уравнения движения
. Из уравнения движения
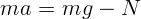 , откуда
, откуда 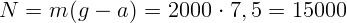 Н. По третьему
закону Ньютона, автомобиль давит на мост с силой, противоположной
Н. По третьему
закону Ньютона, автомобиль давит на мост с силой, противоположной
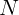 , то есть равной по величине и направленной вниз. Заметим, что
неподвижный автомобиль давил бы с силой
, то есть равной по величине и направленной вниз. Заметим, что
неподвижный автомобиль давил бы с силой 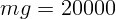 Н, то есть заметно
сильнее. Если еще увеличить скорость, давление может уменьшиться до
нуля. Отрицательным оно не станет, так как автомобиль оторвется от
моста.
Н, то есть заметно
сильнее. Если еще увеличить скорость, давление может уменьшиться до
нуля. Отрицательным оно не станет, так как автомобиль оторвется от
моста.
Разберем задачу, которая позволяет понять, как следует применять
законы Ньютона. Пусть две массы 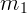 и
и 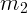 соединены невесомой
нерастяжимой нитью, перекинутой через неподвижный блок (рис. 1.7).
«Неподвижный» значит только, что ось блока закреплена, но вращается на оси
он свободно. Масса блока пренебрежимо мала. Надо найти движение этой
системы, то есть ускорения тел. Удобен стандартный порядок решения
задач:
соединены невесомой
нерастяжимой нитью, перекинутой через неподвижный блок (рис. 1.7).
«Неподвижный» значит только, что ось блока закреплена, но вращается на оси
он свободно. Масса блока пренебрежимо мала. Надо найти движение этой
системы, то есть ускорения тел. Удобен стандартный порядок решения
задач:
1. Сначала изображаются силы, действующие на каждое тело. В данном
случае на 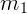 действует сила тяжести
действует сила тяжести 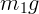 и сила натяжения нити
и сила натяжения нити 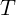 . На
. На
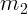 действует
действует 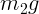 и
и 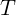 . Мы считаем, что натяжение одинаково вдоль
всей нити. Это следует из ее нулевой массы и из того, что блок не оказывает
сопротивления вращению.
. Мы считаем, что натяжение одинаково вдоль
всей нити. Это следует из ее нулевой массы и из того, что блок не оказывает
сопротивления вращению.
2. Затем необходимо записать уравнения движения, то есть второй закон Ньютона для каждого тела. Если выбрать за положительное направление вниз, то уравнения движения имеют вид

В двух уравнениях три неизвестных: 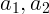 и
и 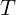 . Нужно еще одно
уравнение. Оно находится из взаимосвязи ускорений тел.
. Нужно еще одно
уравнение. Оно находится из взаимосвязи ускорений тел.
3. Поскольку уравнений движения недостаточно, необходимо выписать
уравнения связей. Используем нерастяжимость нити. Если масса 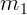 опустилась на 1 м, то на столько же должна подняться масса
опустилась на 1 м, то на столько же должна подняться масса 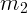 . Модули
смещений одинаковы. Но тогда одинаковы модули скоростей и ускорений. По
направлению же ускорения тел противоположны. Следовательно, недостающее
уравнение имеет вид
. Модули
смещений одинаковы. Но тогда одинаковы модули скоростей и ускорений. По
направлению же ускорения тел противоположны. Следовательно, недостающее
уравнение имеет вид
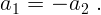
4. Когда полная система уравнений получена, ее нужно решить. Для этого
можно исключать по очереди неизвестные или использовать другие приемы. В
данном случае вместо 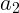 подставляем
подставляем 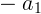 :
:
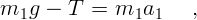
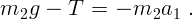
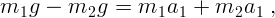
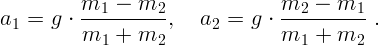
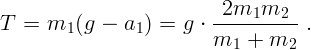
5. Очень важно проанализировать результаты. Прежде всего полезно
проверять размерность. В приведенном решении размерность правильная –
ускорения записаны как 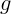 , умноженное на безразмерный коэффициент; сила
имеет размерность массы, умноженной на ускорение. Если размерность ответа
неверна, наверняка в решении есть ошибка.
, умноженное на безразмерный коэффициент; сила
имеет размерность массы, умноженной на ускорение. Если размерность ответа
неверна, наверняка в решении есть ошибка.
Далее важно проверить, не противоречит ли полученное решение здравому
смыслу. В данной задаче, если получается, например, отрицательное
натяжение или ускорение какого-то тела оказалось (при некоторых
значениях масс) больше 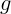 , надо пересмотреть решение и найти ошибку.
Полученный ответ выдерживает такую проверку: всегда (при любых
положительных массах)
, надо пересмотреть решение и найти ошибку.
Полученный ответ выдерживает такую проверку: всегда (при любых
положительных массах) 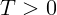 , а ускорения не превышают по абсолютной
величине
, а ускорения не превышают по абсолютной
величине 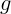 . Это легко понять – нить всегда тянет вверх и замедляет
падение.
. Это легко понять – нить всегда тянет вверх и замедляет
падение.
Важным элементом анализа ответа является рассмотрение предельных
случаев. В нашем решении можно положить, например, 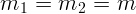 . Тогда
массы должны находиться в равновесии. Это выполняется (получается
. Тогда
массы должны находиться в равновесии. Это выполняется (получается
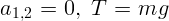 ). Если одна из масс нулевая, вторая должна падать
свободно, с ускорением
). Если одна из масс нулевая, вторая должна падать
свободно, с ускорением 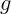 . Это выполняется (положим
. Это выполняется (положим 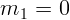 ), что тоже
убеждает в правильности результата. Примерно тот же результат будет,
если масса
), что тоже
убеждает в правильности результата. Примерно тот же результат будет,
если масса 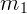 не нулевая, но просто очень мала. При
не нулевая, но просто очень мала. При 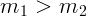 ускорения
ускорения 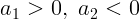 , то есть тяжелое тело опускается, легкое –
поднимается.
, то есть тяжелое тело опускается, легкое –
поднимается.
Анализ не только служит проверкой, но и помогает лучше понять результат,
а иногда и заметить какие-то его особенности. В данной задаче, например,
сила, действующая на подвес блока и равная 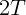 , меньше суммарной
силы тяжести, действующей на тела (если массы не равны). Покажите
это самостоятельно. Попробуйте объяснить физический смысл этого
условия.
, меньше суммарной
силы тяжести, действующей на тела (если массы не равны). Покажите
это самостоятельно. Попробуйте объяснить физический смысл этого
условия.
Рассмотрим тело, которое положили на наклонную плоскость (рис. 1.8).
Пусть задан коэффициент трения 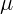 тела о плоскость и угол наклона
тела о плоскость и угол наклона 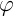 плоскости. Требуется найти, будет ли тело соскальзывать, и если будет, то с
каким ускорением.
плоскости. Требуется найти, будет ли тело соскальзывать, и если будет, то с
каким ускорением.
На тело действует сила тяжести 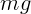 , направленная вниз, сила
нормального давления
, направленная вниз, сила
нормального давления 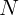 , перпендикулярная плоскости, и сила трения
, перпендикулярная плоскости, и сила трения 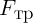 ,
направленная вдоль плоскости вверх. Удобно ввести систему координат с осью
X вдоль плоскости и осью Y перпендикулярно ей. Запишем второй закон
Ньютона в проекциях на эти направления:
,
направленная вдоль плоскости вверх. Удобно ввести систему координат с осью
X вдоль плоскости и осью Y перпендикулярно ей. Запишем второй закон
Ньютона в проекциях на эти направления:
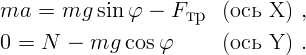
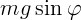 – это проекция силы тяжести на ось X, а величина
– это проекция силы тяжести на ось X, а величина 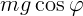 –
это проекция силы тяжести на ось Y.
–
это проекция силы тяжести на ось Y.
Из второго уравнения находится сила нормального давления:
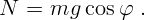
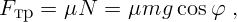
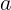 :
:
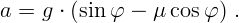
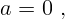
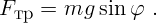
Какой же из вариантов выбрать? Это должно следовать из условий задачи. Необходимо определить, при каких условиях реализуется первый вариант, а при каких – второй.
Рассмотрим случай покоя. Найденная сила трения 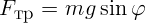 не
должна превышать максимального значения
не
должна превышать максимального значения 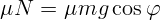 , при котором
наступает проскальзывание. Неравенство
, при котором
наступает проскальзывание. Неравенство
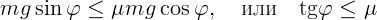
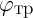 :
:
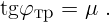
Таким образом, результат задачи следует записать так:
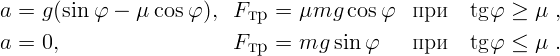
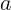 должно быть положительным. Это дает то же самое условие выполнения
варианта:
должно быть положительным. Это дает то же самое условие выполнения
варианта: 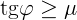 .
.
При угле, равном углу трения, оба решения, конечно, совпадают:
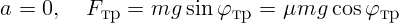 . На практике трение скольжения
может быть несколько меньше трения покоя, так что тело может лежать на
плоскости, но если его толкнуть, будет двигаться вниз с небольшим ускорением.
Подберите такой режим на опыте. Убедитесь, что он получается в узком
интервале углов наклона.
. На практике трение скольжения
может быть несколько меньше трения покоя, так что тело может лежать на
плоскости, но если его толкнуть, будет двигаться вниз с небольшим ускорением.
Подберите такой режим на опыте. Убедитесь, что он получается в узком
интервале углов наклона.
С какой скоростью, направленной вниз, надо бросить мячик с высоты 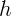 ,
чтобы после удара о пол мячик поднялся на высоту
,
чтобы после удара о пол мячик поднялся на высоту 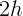 ?
?
Начальная потенциальная энергия мячика 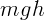 , кинетическая –
, кинетическая – 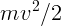 ,
где
,
где 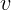 – искомая скорость. После отскока в верхней точке энергия равна
– искомая скорость. После отскока в верхней точке энергия равна
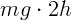 . Закон сохранения энергии:
. Закон сохранения энергии:
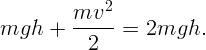
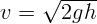 .
.
Два груза массы 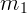 и
и 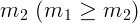 связаны нитью, переброшенной через
неподвижный блок. В начальный момент первый груз удерживают на высоте
связаны нитью, переброшенной через
неподвижный блок. В начальный момент первый груз удерживают на высоте
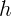 над полом. Затем его без толчка отпускают. Какое количество теплоты
выделится при ударе первого груза о пол?
над полом. Затем его без толчка отпускают. Какое количество теплоты
выделится при ударе первого груза о пол?
Решение
Закон сохранения механической энергии дает
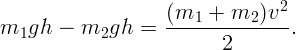
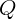 . Тогда
. Тогда
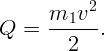
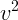 из первого уравнения и подставляя во второе, получим
ответ:
из первого уравнения и подставляя во второе, получим
ответ:
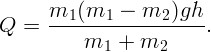
Сила, действующая на снаряд массы 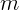 в стволе орудия, нарастает
равномерно от нуля до
в стволе орудия, нарастает
равномерно от нуля до 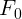 на участке ствола длины
на участке ствола длины 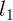 , не меняется на
участке ствола длины
, не меняется на
участке ствола длины 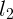 и, наконец, равномерно уменьшается до нуля на
участке ствола длины
и, наконец, равномерно уменьшается до нуля на
участке ствола длины 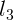 . Какова скорость снаряда при вылете из ствола?
(Рис. 1.9)
. Какова скорость снаряда при вылете из ствола?
(Рис. 1.9)
Из закона сохранения энергии следует, что работа силы действующей на заряд перейдет в его кинетическую энергию.
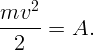
Работу найдем как площадь под графиком функции силы от смещения.
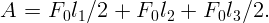
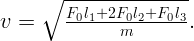
С вершины гладкой полусферы радиуса 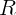 небольшое тело. Найдите его
скорость на высоте
небольшое тело. Найдите его
скорость на высоте 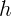 (отсчитываемой от подножья). На какой высоте тело
оторвется от полусферы?
(отсчитываемой от подножья). На какой высоте тело
оторвется от полусферы?
Будем отсчитывать потенциальную энергию от подножья полусферы.
Рассмотрим момент, когда угол между радиусом, проведенным в точку, где
находится тело, и вертикалью равен 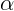 . Тогда высота
. Тогда высота 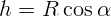 . Из закона
сохранения энергии
. Из закона
сохранения энергии
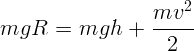
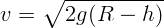 .
.
Рассмотрим динамику движения. По второму закону Ньютона сумма
проекций сил 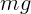 и реакции опоры
и реакции опоры 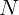 (см. рис. 1.10) должна равняться
произведению массы на центростремительное ускорение:
(см. рис. 1.10) должна равняться
произведению массы на центростремительное ускорение:
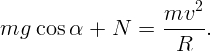
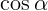 уменьшается. Следовательно,
уменьшается сила реакции. Отрыв тела от поверхности сферы произойдет при
уменьшается. Следовательно,
уменьшается сила реакции. Отрыв тела от поверхности сферы произойдет при
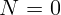 . Подставляя выражение для скорости, получим:
. Подставляя выражение для скорости, получим:
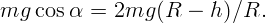
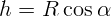 , получаем ответ:
, получаем ответ:
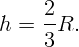
Оцените среднюю силу, приходящуюся на ноги человека при ударе о землю при прыжке со второго этажа.
Выберем высоту второго этажа 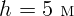 . Тогда скорость при приземлении
тела определится из уравнения
. Тогда скорость при приземлении
тела определится из уравнения
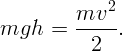
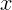 . Эту
величину оценим как
. Эту
величину оценим как 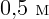 (высота приседания человека). Тогда
(высота приседания человека). Тогда
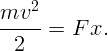
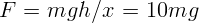 . И, при массе человека 70 кг,
. И, при массе человека 70 кг, 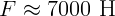 .
.
Груз массы 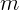 , подвешенный на пружине жесткости
, подвешенный на пружине жесткости 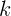 , находится на
подставке. Пружина при этом не деформирована. Подставку быстро убирают.
Определите максимальное удлинение пружины и максимальную скорость
груза.
, находится на
подставке. Пружина при этом не деформирована. Подставку быстро убирают.
Определите максимальное удлинение пружины и максимальную скорость
груза.
В нижнем положении, когда растяжение 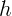 максимально, и скорость равна
нулю, суммарная работа силы тяжести и силы упругости также равна
нулю:
максимально, и скорость равна
нулю, суммарная работа силы тяжести и силы упругости также равна
нулю:
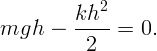
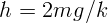 .
.
Скорость тела будет максимальна, когда сумма сил, действующих на тело, равна нулю:
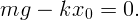
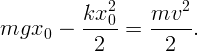
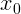 , получим ответ:
, получим ответ:
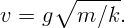
В результате распада движущегося ядра появились два осколка массы 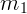 и
и
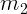 с импульсами
с импульсами 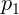 и
и 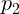 , разлетающиеся под углом
, разлетающиеся под углом 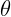 . Определите
выделившуюся при распаде ядра энергию
. Определите
выделившуюся при распаде ядра энергию 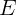 .
.
Пусть 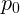 – начальный импульс частицы. Запишем закон сохранения
импульса и энергии:
– начальный импульс частицы. Запишем закон сохранения
импульса и энергии:
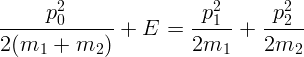
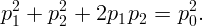
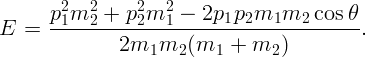
Артиллерист стреляет из пушки ядром массы 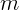 так, чтобы оно упало в
неприятельском лагере. На вылетевшее ядро садится барон Мюнхгаузен, масса
которого
так, чтобы оно упало в
неприятельском лагере. На вылетевшее ядро садится барон Мюнхгаузен, масса
которого 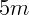 . Какую часть пути до неприятельского лагеря ему придется идти
пешком?
. Какую часть пути до неприятельского лагеря ему придется идти
пешком?
Пусть ядро вылетает со скоростью 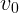 под углом
под углом 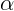 к горизонту. Тогда
дальность полета (расстояние до неприятельского лагеря)
к горизонту. Тогда
дальность полета (расстояние до неприятельского лагеря)
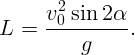
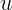 определяется из закона сохранения
импульса:
определяется из закона сохранения
импульса:
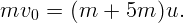
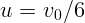 . И ядро пролетит лишь
. И ядро пролетит лишь
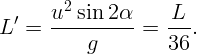
На каком расстоянии (выраженном в радиусах Земли) от Земли на прямой Земля-Луна силы притяжения тела к Земле и Луне равны по величине? Расстояние до Луны в 60 раз больше радиуса Земли. Масса Луны в 81 раз меньше земной.
Пусть 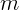 масса рассматриваемого тела, а
масса рассматриваемого тела, а 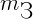 ,
, 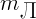 и
и 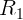 ,
, 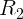 массы и
расстояния от тела до центров Земли и Луны соответственно. Запишем условие
равенства сил притяжения:
массы и
расстояния от тела до центров Земли и Луны соответственно. Запишем условие
равенства сил притяжения:
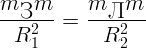
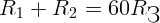
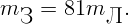
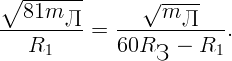
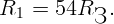
Груз массы 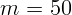 г совершает гармонические колебания с частотой
г совершает гармонические колебания с частотой
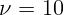 Гц под действием упругой пружины. Найти жесткость пружины.
Гц под действием упругой пружины. Найти жесткость пружины.
Воспользуемся формулой для круговой частоты колебаний тела на пружинне
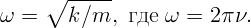
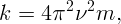
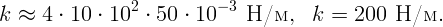
Шарик, подвешенный на длинной нити, отклонили на малый угол и отпустили. В этот же момент времени другой такой же шарик начал свободно падать из точки подвеса нити. Какой из шариков быстрее достигнет точки равновесия первого шарика?
Пусть длина нити равна 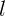 . Тогда первый шарик достигнет положения
равновесия за четверть периода
. Тогда первый шарик достигнет положения
равновесия за четверть периода
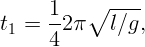
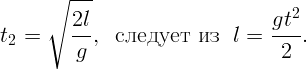
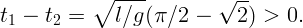
Раздел механики статика рассматривает условия равновесия тел. Легко придумать два необходимых условия равновесия, которые будут всегда выполняться в случае равновесия.
Найти силу натяжения троса в системе изображенной на рисунке 1.11.
В данном случае, для решения задачи достаточно воспользоваться только
первым условием равновесия – балансом сил. В качестве рассматриваемого тела
удобно выбрать небольшой кусок троса в области подвеса груза, точка 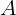 .
Сумма векторов сил прикладываемых к этой точке должна давать ноль.
Запишем уравнение для проекций сил на вертикальную ось, явно указав знаки
компонент.
.
Сумма векторов сил прикладываемых к этой точке должна давать ноль.
Запишем уравнение для проекций сил на вертикальную ось, явно указав знаки
компонент.
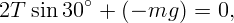
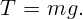
Цепочка массы 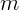 подвешена за концы так, что вблизи точек подвеса она
образует с горизонталью угол
подвешена за концы так, что вблизи точек подвеса она
образует с горизонталью угол 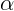 . Определите силу натяжения цепочки в ее
нижней точке и в точках подвеса (рис. 1.12, а).
. Определите силу натяжения цепочки в ее
нижней точке и в точках подвеса (рис. 1.12, а).
Для определения натяжения цепочки в точках подвеса приравняем нулю сумму вертикальных проекций сил (рис. 1.12, б)
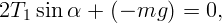
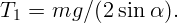
Для определения натяжения в нижней точке рассмотрим половину цепочки и приравняем сумму горизонтальных проекций сил нулю (рис. 1.12, в).
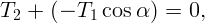
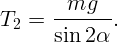
Попробуем приставить однородный стержень длины 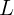 наклонно к стене
комнаты.
наклонно к стене
комнаты.
Пусть стержень составляет угол 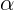 с горизонтом и пол гладкий, то
есть трения между стержнем и полом нет (рис. 1.13, а). Возможно ли
равновесие?
с горизонтом и пол гладкий, то
есть трения между стержнем и полом нет (рис. 1.13, а). Возможно ли
равновесие?
На рисунке изображены силы, которые должны действовать на стержень со
стороны Земли (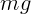 ), стенки (
), стенки (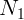 и
и 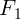 ) и пола (
) и пола (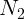 ). Очевидно,
что на ось X имеет отличную от нуля проекцию единственная сила –
). Очевидно,
что на ось X имеет отличную от нуля проекцию единственная сила –
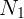 . Тогда уравнение равновесия сил может быть выполнено лишь
при
. Тогда уравнение равновесия сил может быть выполнено лишь
при 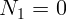 . Следовательно, сила трения
. Следовательно, сила трения 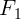 также равна нулю, а
также равна нулю, а
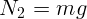 .
.
Но тогда условие равенства нулю суммы моментов сил не выполняется.
Выбрав ось вращения, например, проходящей через центр стержня, получим
для момента силы 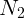 :
:
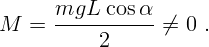
Пусть между стержнем и полом есть трение, а стена гладкая. Возможно ли равновесие теперь?
Силы, действующие в этом случае, изображены на рисунке 1.13, б). Здесь
через 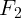 обозначена сила трения. Условие равновесия сил в проекциях на оси
X и Y дает:
обозначена сила трения. Условие равновесия сил в проекциях на оси
X и Y дает:
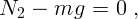
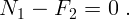
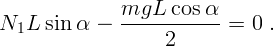
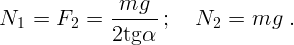
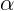 мал, и сила трения
мал, и сила трения 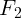 из этого решения получится
очень большой. Однако она не может превышать значения
из этого решения получится
очень большой. Однако она не может превышать значения 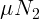 – силы
трения скольжения:
– силы
трения скольжения:
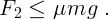
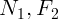 могут выполняться лишь при углах
не меньше некоторого критического
могут выполняться лишь при углах
не меньше некоторого критического 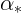 . Значение критического угла
соответствует случаю, когда сила трения покоя максимальна:
. Значение критического угла
соответствует случаю, когда сила трения покоя максимальна:
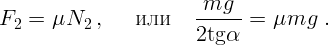
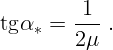
Если попытаться установить стержень с меньшим углом, то есть ближе к
горизонтальному положению, то формально равновесие возможно только при
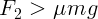 . Этого можно добиться, только удерживая стержень в нижней
точке дополнительной внешней силой. Одно же трение будет неспособно
обеспечить устойчивость, и стержень упадет.
. Этого можно добиться, только удерживая стержень в нижней
точке дополнительной внешней силой. Одно же трение будет неспособно
обеспечить устойчивость, и стержень упадет.
Для записи условия равновесия моментов сил в рассмотренной задаче можно было выбрать и любую другую ось. Так, для оси, проходящей через верхнюю точку стержня, для рис. 1.13, б) получим:
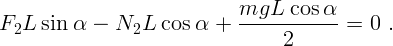
Если тело не вращается (как должно быть в статике), то оно не вращается
относительно любой неподвижной оси. Разумно выбирать ось так, чтобы
уравнение моментов было максимально простым. Выбрав ось проходящей через
точку O, мы автоматически обратили моменты двух из четырех сил в нуль, так
как плечи сил 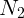 и
и 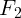 равны нулю.
равны нулю.