Оглавление

2 Молекулярно-кинетическая теория
 2.1 Строение вещества. Уравнение состояния
  2.1.1 Пример – количество атомов
  2.1.2 Пример – химический состав
  2.1.3 Пример – воздух в комнате
  2.1.4 Пример – воздушный шар
 2.2 Термодинамика
  2.2.1 Пример – давление и энергия идеального газа
  2.2.2 Пример – работа, тепло и внутренняя энергия
  2.2.3 Пример – работа и КПД цикла
  2.2.4 Пример – динамическое отопление
 2.3 Фазовые переходы. Поверхностное натяжение
  2.3.1 Пример – нагревание и кипение воды
  2.3.2 Пример – «пограничное» кипение
  2.3.3 Пример – влажность воздуха
  2.3.4 Пример – капля ртути

Глава 2
Молекулярно-кинетическая теория

2.1 Строение вещества. Уравнение состояния

2.1.1 Пример – количество атомов

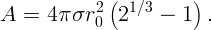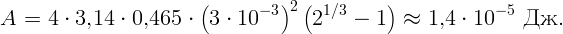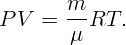
Плотность алюминия 2,7 ⋅ 103 кг/м3. Сколько атомов алюминия содержится в объеме 1 см3? Молекулярная масса алюминия 27 ⋅ 10-3 кг/моль.

Решение

Один моль (27 г) алюминия содержит 6 ⋅ 1023 атомов. В 1 см3 содержится 2,7 г, то есть в 10 раз меньше.

Ответ: 6 ⋅ 1022 атомов.

2.1.2 Пример – химический состав

Найдите формулу соединения азота с кислородом, если его масса m = 1 г в газообразном состоянии в объеме V = 1 л создает при температуре T = 17∘C давление P = 3,17 ⋅ 104 Па.

Решение

Давление определяется из уравнения состояния идеального газа

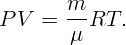
P V = m--RT . μ
Определим молекулярную массу соединения
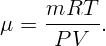
mRT μ = ------. P V
Подставим числа, выразив их в системе единиц СИ: m = 1 г = 10-3 кг, R = 8,31 Дж/(моль⋅К), V = 1 л = 10-3 м3, P = 3,17 ⋅ 104 Па, T = 290 К. Отсюда
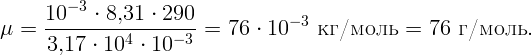
- 3 μ = 10----⋅-8,31-⋅ 290 = 76 ⋅ 10- 3 кг/ мо ль = 76 г/м ол ь. 3,17 ⋅ 104 ⋅ 10 - 3
Пусть в соединении содержится x атомов азота и y атомов кислорода. Молекулярная масса азота 14 г/моль, кислорода. 16 г/моль. Тогда должно выполняться равенство:
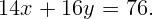
14x + 16y = 76.
Так как x и y - целые числа, легко найти, что x = 2,y = 3.

Ответ: соединение N2O3.

2.1.3 Пример – воздух в комнате

Температура воздуха в комнате объемом V = 45 м3 повысилась от t1 = 17∘C до t2 = 27∘C. На сколько уменьшилась масса воздуха в комнате? Атмосферное давление P0 = 105 Па постоянно. Молекулярная масса воздуха μ = 29 г/моль.

Решение

Пусть m1 масса воздуха, соответствующая начальной температуре T1 = 290 K, а m2 – конечной T2 = 300 K. Запишем уравнения состояния газа для начального и конечного состояний:

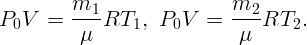
P V = m1--RT , P V = m2--RT . 0 μ 1 0 μ 2
Искомая масса воздуха Δm = m1 - m2.

Выражая массы из первых двух уравнений и подставляя в третье, получим

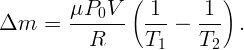
μP V ( 1 1 ) Δm = ----0-- --- - --- . R T1 T2
Подставив числа, получим ответ Δm = 1,8 кг.

2.1.4 Пример – воздушный шар

Во сколько раз изменится подъемная сила воздушного шара, если наполняющий его гелий заменить водородом? Весом оболочки шара пренебречь.

Решение

Пусть атмосферное давление P, температура T, объем воздушного шара V . Масса воздуха, содержащаяся при этих условиях в объеме V , определится из уравнения состояния

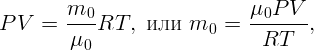
m0-- μ0P-V-- P V = μ RT , и ли m0 = RT , 0
где μ0 – молекулярная масса воздуха. Обозначим через μ1 молекулярную массу водорода, а через μ2 – молекулярную массу гелия. Тогда массы водорода m1 и гелия m2, содержащихся в объеме V , выразятся соотношениями
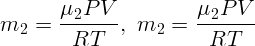
m = μ2P-V--, m = μ2P--V- 2 RT 2 RT
Соответствующие подъемные силы определятся разницей веса воздуха и газа в объеме V :
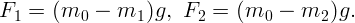
F = (m - m )g, F = (m - m )g. 1 0 1 2 0 2
Подставив в последние уравнения выражения масс, получим для отношения подъемных сил
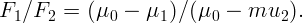
F1∕F2 = (μ0 - μ1 )∕(μ0 - mu2 ).
Подставляя численные значения μ0 = 29 г/моль, μ1 = 2 г/моль, μ2 = 4 г/моль, получим
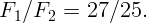
F1 ∕F2 = 27 ∕25.

2.2 Термодинамика

2.2.1 Пример – давление и энергия идеального газа

Одноатомный идеальный газ изотермически расширяется из состояния с давлением P = 105 Па от объема V 1 = 1 м3 до объема V 2 = 5 м3. Какова внутренняя энергия и давление газа в конечном состоянии?

Решение

Внутренняя энергия идеального газа при изотермическом расширении не меняется. Поэтому ее можно найти из начального состояния. Для одноатомного газа

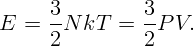
3 3 E = --N kT = --P V. 2 2
И из данных задачи получаем
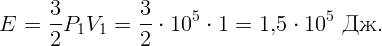
E = 3P V = 3-⋅ 105 ⋅ 1 = 1,5 ⋅ 105 Д ж. 2 1 1 2
При постоянной температуре P1V 1 = P2V 2. Откуда конечное давление
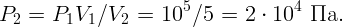
5 4 P2 = P1V1 ∕V2 = 10 ∕5 = 2 ⋅ 10 П а.

2.2.2 Пример – работа, тепло и внутренняя энергия

Газ в цилиндре получил тепло Q = 1000 Дж и, расширившись, совершил работу A = 300 Дж. На сколько изменилась при этом его внутренняя энергия?

Решение

Согласно первому закону термодинамики изменение внутренней энергии газа равно количеству тепла, полученного газом, минус работа, совершенная газом: ΔE = Q - ΔA.

Откуда ΔE = 1000 - 300 = 700 Дж.

2.2.3 Пример – работа и КПД цикла

Один моль одноатомного идеального газа участвует в циклическом процессе, график которого, состоящий из двух изохор и двух изобар, представлен на рисунке 2.1. Температуры в точках 1 и 3 равны T1 и T3. Известно, что точки 2 и 4 лежат на одной изотерме. Определите работу, совершенную газом за цикл и КПД цикла.

PIC

Рис. 2.1:

Решение

Обозначим через V 1 минимальный объем, занимаемый газом (на изохоре 1,2), через V 2 – максимальный (на изохоре 3,4). Соответственно, через P1 – минимальное (на изобаре 4,1), а через P2 – максимальное (на изобаре 2,3) давление. Пусть температура в точках 2 и 3 равна T2.

Работа газа за цикл определится как площадь на диаграмме:

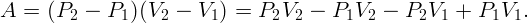A = (P2 - P1 )(V2 - V1) = P2V2 - P1V2 - P2V1 + P1V1.
(2.1)

Из уравнения состояния идеального газа для одного моля имеем:

P2V2 = RT3 (2.2) P1V2 = RT2 (2.3) P2V1 = RT2 (2.4) P1V1 = RT1. (2.5)
Подставляя (2.2) – (2.5) в (2.1), получим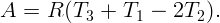
A = R (T3 + T1 - 2T2 ).
Теперь необходимо найти T2. Для этого разделим почленно (2.2) на (2.3), а (2.4) на (2.5):
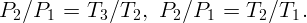
P2 ∕P1 = T3∕T2, P2 ∕P1 = T2∕T1.
Приравнивая правые части
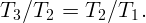
T3 ∕T2 = T2 ∕T1.
Откуда
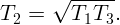
√ ------ T2 = T1T3.
Работа газа определится через заданные температуры
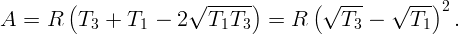
( √ -----) (√ --- √ ---)2 A = R T3 + T1 - 2 T1T3 = R T3 - T1 .
Найдем теперь КПД цикла. Для этого надо найти тепло, переданное газу за цикл – Q. Газ получает от нагревателя тепло на участках 1,2 и 2,3. На остальных участках газ отдает тепло холодильнику.

При изохорическом процессе тепло, полученное газом:

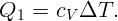
Q1 = cV ΔT .
Для одного моля одноатомного идеального газа cV = 3R∕2. Тогда
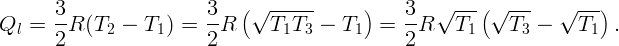
3 3 (√ ------ ) 3 √ ---(√ --- √ --) Ql = --R (T2 - T1 ) = --R T1T3 - T1 = --R T1 T3 - T1 . 2 2 2
При изобарическом расширении газ получает тепло
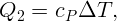
Q = c ΔT , 2 P
где cP = cV + R = 3R∕2 + R = 5R∕2. То есть
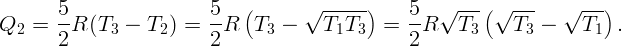
5- 5- ( √ -----) 5- √ ---(√ --- √ ---) Q2 = R (T3 - T2 ) = R T3 - T1T3 = R T3 T3 - T1 . 2 2 2
Полное количество тепла, полученного газом
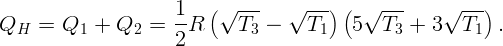
1- (√ --- √ ---) ( √ --- √ ---) QH = Q1 + Q2 = R T3 - T1 5 T3 + 3 T1 . 2
КПД цикла
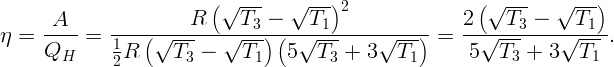
(√ --- √ ---) (√ --- √ --) A R T - T 2 2 T - T η = ---- = ----(√--------√--3)-(--√-1------√----) = --√----3----√--1--. QH 12 R T3 - T1 5 T3 + 3 T1 5 T3 + 3 T1
Пусть T3 = 900 K, T1 = 400 K. Тогда
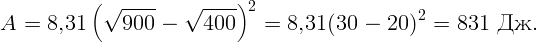
( √ ----- √ ----)2 2 A = 8,31 900 - 400 = 8,31 (30 - 20) = 831 Д ж.
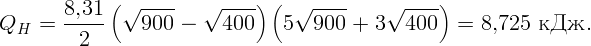
(√ ----- √ ----) ( √ ----- √ ----) Q = 8,31- 900 - 400 5 900 + 3 400 = 8,725 кД ж. H 2
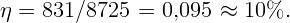
η = 831 ∕8725 = 0,095 ≈ 10%.
Заметим, что КПД обратимой машины, работающей с нагревателем температуры T3 = 900 K, и холодильником с T1 = 400 K определится из формулы
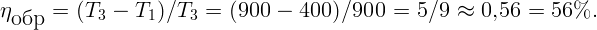
ηо бр = (T3 - T1 )∕T3 = (900 - 400 )∕900 = 5∕9 ≈ 0,56 = 56%.

2.2.4 Пример – динамическое отопление

С помощью электрической плитки мощностью N = 1 кВт в комнате поддерживается температура воздуха t1 = 17∘C при температуре наружного воздуха t2 = -23∘C. Какая мощность потребовалась бы для поддержания в комнате той же температуры с помощью обратимой тепловой машины?

Решение

Для поддержания нужной температуры запустим тепловую машину по обратному циклу. Тогда наружный воздух будет играть роль нагревателя при T2 = 250 K, а воздух в комнате – роль холодильника при T1 = 290 K. Процесс пойдет таким образом: забрав тепло Q2 от наружного воздуха и затратив некоторую работу A (например, с помощью электродвигателя), передадим тепло Q1 внутрь комнаты. Пусть A, Q1 и Q2 относятся к единице времени (секунде). Тогда для поддержания той же температуры необходимо, чтобы переданное тепло Q1 равнялось теплу, поступающему в первом случае:

Q1 = N.
КПД тепловой машины
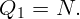
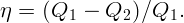
η = (Q1 - Q2 )∕Q1.
Так как машина обратимая
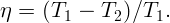
η = (T1 - T2)∕T1.
Приравнивая правые части последних выражений, получим
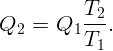
Q = Q T2-. 2 1T1
Мощность, которую необходимо затратить
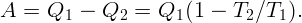
A = Q1 - Q2 = Q1 (1 - T2 ∕T1 ).
Подставляя Q1 = 103 Вт и температуры, получим
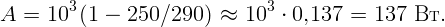
A = 103(1 - 250 ∕290 ) ≈ 103 ⋅ 0,137 = 137 В т.
При таком способе отопления затрачивается значительно меньше энергии! Вместо электрической мощности 1 кВт можно затрачивать для работы электродвигателя лишь 137 Вт. Такое отопление называется «динамическим». Идею использования динамического отопления выдвинул лорд Кельвин.

2.3 Фазовые переходы. Поверхностное натяжение

2.3.1 Пример – нагревание и кипение воды

В кастрюлю налили воду при температуре t0 = 10∘C и поставили на плиту. Через τ = 10 минут вода закипела. Через какое время она полностью превратится в пар?

Решение

Обозначим через c удельную теплоемкость воды. Будем считать, что теплоемкость при росте температуры не меняется: c = 1 кал/(г⋅град) = 4,18 ⋅ 103 Дж/(кг⋅град).

Пренебрежем потерями тепла, считая, что за единицу времени при любой температуре воде передается одинаковая энергия w. Пусть масса воды m. Тогда за время τ вода получила энергию wτ, которая пошла на нагревание до температуры кипения t = 100∘ C:

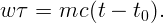w τ = mc (t - t ). 0
(2.1)

Для того, чтобы вода выкипела, она должна получить энергию mq, где q = 2,26 ⋅ 106 Дж/кг – удельная теплота парообразования воды. Такое тепло вода получит за время τ1:

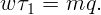w τ1 = mq.
(2.2)

Выразив массу из (2.1) и подставив в (2.2) получаем

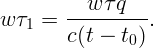
---w-τq--- w τ1 = . c (t - t0)
Откуда
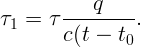
τ = τ ---q----. 1 c(t - t0
Подставляя числа
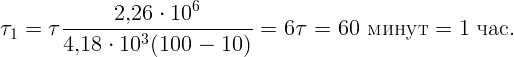
6 τ = τ-------2,26-⋅ 10------- = 6τ = 60 м ину т = 1 ча с. 1 4,18 ⋅ 103 (100 - 10 )

Ответ: вода полностью выкипит через час после закипания.

2.3.2 Пример – «пограничное» кипение

В стакан налиты две несмешивающихся жидкости: четыреххлористый углерод (CCl4) и вода. При нормальном атмосферном давлении CCl4 кипит при 76,7∘C, вода – при 100∘C. При равномерном нагревании стакана со смесью в водяной бане кипение на границе раздела жидкостей начинается при температуре 65,5∘С. Определите, какая из жидкостей быстрее (по массе) выкипает при таком «пограничном» кипении и во сколько раз. Давление насыщенного пара воды при 65,5∘С составляет 25,6 кПа.

Решение

При пограничном кипении газовые пузырьки растут на границе раздела жидкостей. При этом сумма парциальных давлений CCl4 (P1) и воды (P2 = 25,6 кПа) должна равняться атмосферному давлению (при нормальных условиях P0 = 1 атм = 100 кПа):

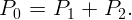P = P + P . 0 1 2
(2.1)

Масса m1 четыреххлористого углерода, находящегося в некотором пузырьке объема V , определится из уравнения Клапейрона-Менделеева:

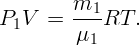m1 P1V = ----RT . μ1
(2.2)

Здесь μ1 = 154 г/моль – молекулярная масса CCl4, T = 338,5 K – абсолютная температура, соответствующая 65,5∘C. Аналогично для воды

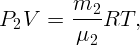P V = m2-RT , 2 μ2
(2.3)

где μ2 = 18 г/моль.

Разделив почленно (2.2) на (2.3), имеем

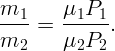m1 μ1P1 ----= ------. m2 μ2P2
(2.4)

Подставив в (2.4) давление P1, выраженное из (2.1), получим

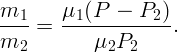
m1-- = μ1(P-----P2-). m2 μ2P2
Подставив числа, получим ответ
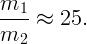
m1 ---- ≈ 25. m2

2.3.3 Пример – влажность воздуха

При одинаковой температуре смешали (объединив объемы) V 1 = 1 м3 воздуха влажностью φ1 = 20% и V 2 = 2 м3 воздуха влажностью φ2 = 30%. Определите относительную влажность смеси.

Решение

Обозначим давление насыщенного пара при температуре T через P0, парциальное давление водяного пара массы m1 в объеме V 1 = 1 м3 – через P1, а водяного пара массы m2 в объеме V 2 = 2 м3 – через P2.

По определению влажность (выраженная не в процентах) в первом объеме

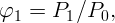φ = P ∕P , 1 1 0
(2.1)

а во втором

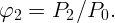φ2 = P2 ∕P0.
(2.2)

Параметры водяного пара в каждом случае определятся из уравнения Клапейрона-Менделеева

P V = m1RT , (2.3) 1 1 μ P2V2 = m2RT . (2.4) μ
После объединения объемов установится парциальное давление водяного пара P, определяемое из уравнения
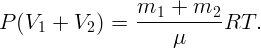m + m P (V1 + V2 ) = --1------2RT . μ
(2.5)

Выразив из (2.1) и (2.2) P1 = φ1P0 и P2 = φ2P0, а также m1 и m2 из (2.3) и (2.4) и подставив все в (2.5), получим

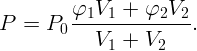
P = P φ1V1--+-φ2V2--. 0 V1 + V2
Относительная влажность воздуха определится как
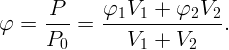
φ = P--= φ1V1--+--φ2V2--. P0 V1 + V2
Подставляя числа
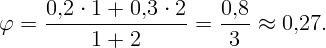
φ = 0,2-⋅ 1-+-0,3-⋅ 2-= 0,8-≈ 0,27. 1 + 2 3
Так как относительная влажность воздуха выражается в процентах, ответ φ ≈ 27%.

2.3.4 Пример – капля ртути

Какую работу против сил поверхностного натяжения нужно совершить, чтобы разделить сферическую каплю ртути радиуса r0 = 3 мм на две одинаковые капли? Коэффициент поверхностного натяжения ртути σ = 0,465 Н/м.

Решение

Работа против сил поверхностного натяжения определяется изменением полной поверхности

A = σ ΔS.
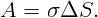(2.1)

Начальная поверхность S0 = 4πr02. Обозначим радиус каждой из двух образовавшихся капель через r. Тогда полная поверхность двух капель S = 2 ⋅ 4πr2. Так как ΔS = S - S0, работа

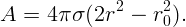2 2 A = 4π σ (2r - r0).
(2.2)

При разделении капли сохраняется полный объем ртути

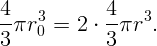4-πr3 = 2 ⋅ 4-πr3. 3 0 3
(2.3)

Откуда находится радиус образовавшихся капель. Подставив r из (2.3) в (2.2), получим

A = 4π σr2 (21∕3 - 1) . 0
Подставляя числа, получим ответ
( ) ( ) A = 4 ⋅ 3,14 ⋅ 0,465 ⋅ 3 ⋅ 10 - 3 2 21 ∕3 - 1 ≈ 1,4 ⋅ 10 - 5 Д ж.