Оглавление

Глава 4
Волны, оптика, строение вещества

4.1 Переменный ток

4.1.1 Пример – амплитудное и действующее значение тока

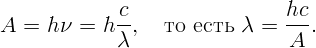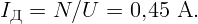
Найдите амплитудное и действующее значение тока, протекающего через электрическую лампочку мощности N = 100 Вт, включенную в сеть с напряжением U = 220 В.

Решение

Напряжение 220 В – действующее. Мощность N = U_дI_д. Откуда

4.1.2 Пример – две электроплитки

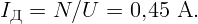
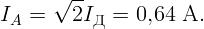
Две одинаковые электрических плитки мощности N = 1 кВт включаются в электрическую сеть а) параллельно; б) последовательно. Найдите суммарную мощность плиток в первом и во втором случаях.

Решение

Сопротивления плиток R одинаковы. Обозначим напряжение сети через U. Тогда из условия N = U²∕R. И R = U²∕N.

При параллельном соединении плиток полное сопротивление R₁ = R∕2. И

4.1.3 Пример – резонанс в контуре

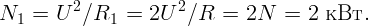
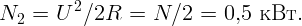
Резонанс наблюдается в колебательном контуре при частоте ν = 400 Гц. Емкость конденсатора в контуре C = 1 мкФ. Какую емкость нужно подсоединить параллельно данной, чтобы частота резонанса уменьшилась до 100 Гц?

Решение

Резонансная частота определяется формулой:

4.1.4 Пример – токи при разрядке конденсатора

Рис. 4.1:

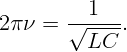
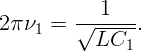
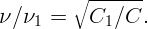
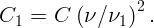
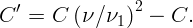
Конденсатор емкости C заряжен зарядом q₀. Параллельно подсоединены две катушки индуктивности L₁ и L₂ (см. рис. 4.1). Ключ K замыкают. Найдите максимальные значения силы токов через катушки.

Решение

По закону Кирхгофа падение напряжения на катушках одинаково:

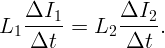
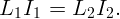(4.1)

Тогда ясно, что максимальное значение силы токов в катушках достигается одновременно. Запишем закон сохранения энергии (при максимальном значении силы тока конденсатор не заряжен):

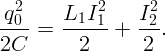(4.2)

Выражая из (4.1) I₂ и подставляя в (4.2), получим:

4.2 Геометрическая оптика

4.2.1 Пример – фонарь и тени

Рис. 4.2:

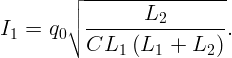
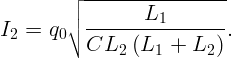
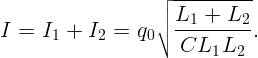
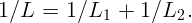
На какой высоте H висит уличный фонарь, если тень от вертикально стоящей палки высотой h = 1 м имеет длину l = 1,5 м, а если палку поставить в конец тени, то новая длина тени L = 2,5 м?

Решение

Пусть x – начальное расстояние от подножья фонаря до палки. Тогда из рисунка 4.2, сравнивая подобные треугольники, имеем:

4.2.2 Пример – преломление луча

Рис. 4.3:

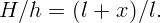
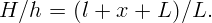
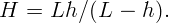
Под каким углом должен падать световой луч на стекло, чтобы угол между отраженным и преломленным лучами был прямым? Показатель преломления стекла n.

Решение

Из рисунка следует α + β + π∕2 = π. И sin α∕ sin β = n. Тогда из первого уравнения имеем:

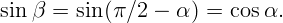
Ответ α = arctg n.

4.2.3 Пример – фокусное расстояние системы линз

Две тонкие линзы с фокусными расстояниями F₁ и F₂ стоят вплотную друг к другу. Найдите фокусное расстояние такой системы.

Решение

ЋЗабудемЛ пока о второй линзе. Пусть расстояние от источника до первой линзы a₁. Тогда изображение, даваемое первой, линзой окажется на расстоянии

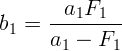
Источник света для второй линзы будет находиться на расстоянии

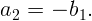
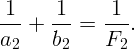
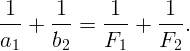
Иными словами, оптические силы вплотную сложенных тонких линз складываются:

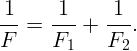
Эту задачу можно решить проще. Поместим точечный источник в фокус первой линзы. Тогда после преломления в ней лучи станут параллельными. После преломления во второй линзе они пересекутся ее фокусе. То есть

4.2.4 Пример – увеличенное изображение

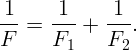
Расстояние от предмета до экрана L = 1,8 м. Линзу с каким фокусным расстоянием надо взять и где следует ее поставить, чтобы получить изображение предмета, увеличенное в два раза?

Решение

Запишем формулу линзы:

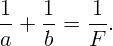
Решая систему уравнений, получим ответ: F = 0,4 м, a = 0,6 м.

4.3 Волновая оптика

4.3.1 Пример – скорость света в стекле

Длина волны света в стекле λ = 0,48 мм при частоте ν = 4 ⋅ 10¹⁴ Гц. Чему равна скорость света в стекле?

Решение

Скорость света определится из формулы v = νλ. Подставляя числа, получаем v = 1,92 ⋅ 10⁸ м/с.

4.3.2 Пример – интерференция двух источников

Два когерентных источника света S₁ и S₂ освещают экран, плоскость которого параллельна S₁S₂. Чему равна длина волны света, если расстояние между двумя соседними максимумами освещенности на экране Δx равно 1,2 мм? Расстояние до экрана L = 4,8 м, а между источниками света d = 2 мм.

Решение

Расстояние между соседними максимумами определится по формуле

4.3.3 Пример – дифракционная решетка

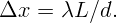
Дифракционная решетка имеет 250 штрихов на 1 мм. На решетку падает монохроматический свет с длиной волны 500 нм. Под каким углом виден первый максимум?

Решение

Для первого максимума имеем sin φ = λ∕d. Подставляя числа, получим sin φ = 0,125. Откуда φ = 7,2^∘.

4.4 Специальная теория относительности

4.4.1 Пример – время жизни движущейся частицы

В состоянии покоя частица живет время τ₀ = 10^-6 с. Какое расстояние она пролетит до распада при скорости v = 2,5 ⋅ 10⁸ м/с?

Решение.

В лабораторной системе отсчета время

4.4.2 Пример – полная энергия движущейся частицы

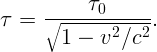
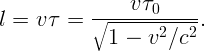
При какой скорости частицы ее полная энергия вдвое превосходит энергию покоя?

Решение

По условию

4.5 Квантовая физика

4.5.1 Пример – энергия кванта излучения

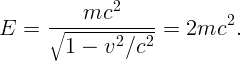
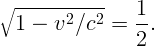
Определите энергию кванта излучения с длиной волны λ = 5 ⋅ 10^-7 м.

Решение

По формуле Планка энергия кванта определяется как

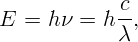
где h – постоянная Планка, c – скорость света, λ – длина волны. Подставляя численные значения, получим:

4.5.2 Пример – красная граница фотоэффекта

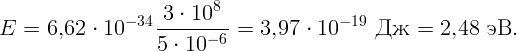
Определите красную границу фотоэффекта для цинка. Работа выхода электрона A = 4,24 эВ.

Решение

Из уравнения Эйнштейна работа выхода равна энергии кванта: