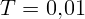 с, амплитудой
с, амплитудой
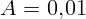 м. Найти максимальную скорость и максимальное ускорение тела.
м. Найти максимальную скорость и максимальное ускорение тела.
1.1.1. Тело совершает колебания с периодом 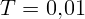 с, амплитудой
с, амплитудой
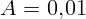 м. Найти максимальную скорость и максимальное ускорение тела.
м. Найти максимальную скорость и максимальное ускорение тела.
1.1.2. Тело совершает гармонические колебания с амплитудой 0,1 м, периодом
0,02 с, начальной фазой 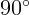 . Найти амплитудные значения скорости и ускорения
тела. Чему будут равны координата, скорость и ускорение при
. Найти амплитудные значения скорости и ускорения
тела. Чему будут равны координата, скорость и ускорение при 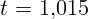 с?
с?
1.1.3. Тело, прикрепленное к некоторой пружине, отклонили на расстояние 1 см
от положения равновесия и отпустили, частота его собственных колебаний
составляет 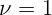 Гц, трение пренебрежимо мало. Какой путь пройдет тело
за 0,01 с, 0,1 с, 0,5 с, 1 с, 2 с? Какое будет при этом перемещение тела?
Гц, трение пренебрежимо мало. Какой путь пройдет тело
за 0,01 с, 0,1 с, 0,5 с, 1 с, 2 с? Какое будет при этом перемещение тела?
1.1.4. Груз массы 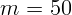 г совершает гармонические колебания с частотой
г совершает гармонические колебания с частотой
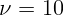 Гц под действием упругой пружины. Найти жесткость пружины.
Гц под действием упругой пружины. Найти жесткость пружины.
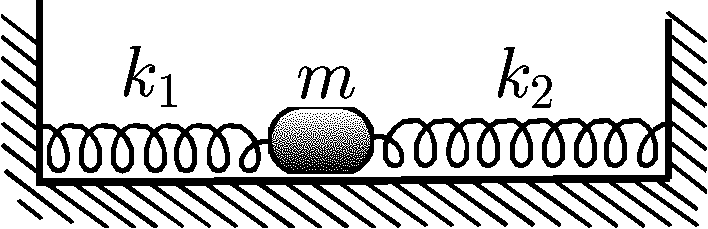
 1.1.5. Тело массы
1.1.5. Тело массы 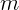 находится на гладком столе и прикреплено к двум
горизонтальным пружинам жесткости
находится на гладком столе и прикреплено к двум
горизонтальным пружинам жесткости 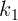 и
и 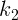 , другие концы пружин
закреплены. Сумма длин недеформированных пружин равна расстоянию между
точками их закрепления. Тело отклоняют из положения равновесия вдоль пружин и
отпускают. Найти период колебаний.
, другие концы пружин
закреплены. Сумма длин недеформированных пружин равна расстоянию между
точками их закрепления. Тело отклоняют из положения равновесия вдоль пружин и
отпускают. Найти период колебаний.
1.1.6. Длина маятника в Исаакиевском соборе в Санкт-Петербурге равна 98 м. Чему равен период колебаний этого маятника?
1.1.7. Как изменятся показания маятниковых часов, если перевезти их с Земли на Луну? Ускорение свободного падения на Луне примерно в 6 раз меньше, чем на Земле.
1.1.8. Один из математических маятников совершил 10 колебаний за определенный промежуток времени, другой — 6. Найти длины маятников, если известно, что один из них длиннее другого на 16 см.
1.1.9. Шарик, подвешенный на длинной нити, отклонили на малый угол и отпустили. В этот же момент времени другой такой же шарик начал свободно падать из точки подвеса нити. Какой из шариков быстрее достигнет точки равновесия первого шарика?
1.1.10. Масса маятника составляет 100 г, длина нити — 1 м, максимальное
отклонение от положения равновесия — 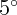 . Найти энергию колебаний маятника.
. Найти энергию колебаний маятника.
1.1.11. Маятник с нитью длины 0,5 м в начальный момент времени отклонили
на угол 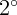 и придали ему скорость 1 м/с в направлении положения равновесия.
Найти амплитуду и начальную фазу колебаний маятника.
и придали ему скорость 1 м/с в направлении положения равновесия.
Найти амплитуду и начальную фазу колебаний маятника.
1.1.12. Тело массы 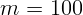 г подвешено в поле тяжести на вертикальной
пружине жесткости
г подвешено в поле тяжести на вертикальной
пружине жесткости 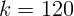 Н/м. В начальный момент времени растяжение
пружины
Н/м. В начальный момент времени растяжение
пружины 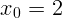 см, а скорость тела равна нулю. Найти период, амплитуду, фазу и
энергию вертикальных колебаний. Как изменится ответ, если начальное растяжение
будет 0,5 см?
см, а скорость тела равна нулю. Найти период, амплитуду, фазу и
энергию вертикальных колебаний. Как изменится ответ, если начальное растяжение
будет 0,5 см?
1.1.13. Два тела одинаковой массы 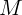 , находящиеся на горизонтальной
плоскости, соединены невесомой пружиной жесткости
, находящиеся на горизонтальной
плоскости, соединены невесомой пружиной жесткости 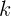 и совершают
колебательное движение вдоль пружины. Найти период колебаний. Трением
пренебречь.
и совершают
колебательное движение вдоль пружины. Найти период колебаний. Трением
пренебречь.
1.1.14. Рассмотреть предыдущую задачу для случая разных масс 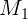 и
и 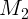 .
.
 1.1.15. В
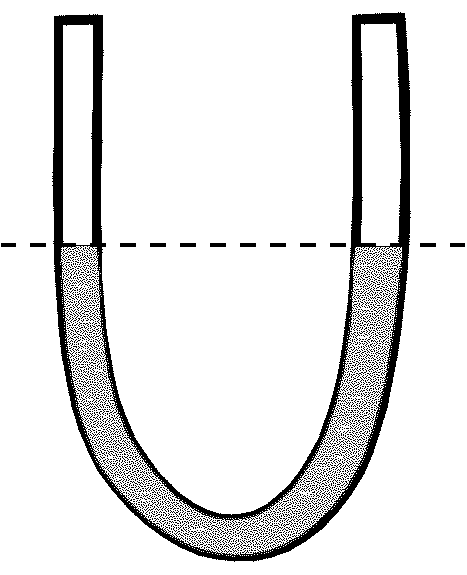
1.1.15. В 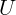 -образную трубку постоянного сечения
-образную трубку постоянного сечения 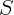 , находящуюся в
вертикальном положении, налита жидкость плотности
, находящуюся в
вертикальном положении, налита жидкость плотности 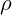 . Длина участка трубки,
занятого жидкостью, равна
. Длина участка трубки,
занятого жидкостью, равна 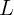 . Найти период колебаний жидкости в трубке, если
трение пренебрежимо мало.
. Найти период колебаний жидкости в трубке, если
трение пренебрежимо мало.
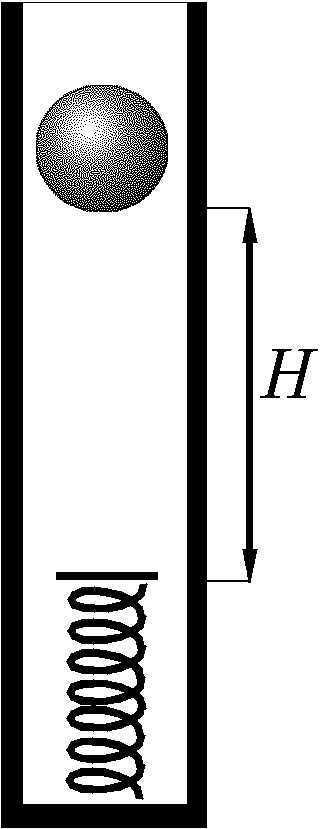
 1.1.16. По гладкой вертикальной трубе может без трения двигаться шарик
массы
1.1.16. По гладкой вертикальной трубе может без трения двигаться шарик
массы 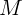 . На дне трубы находится невесомая пружина жесткости
. На дне трубы находится невесомая пружина жесткости 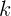 . В
начальный момент шарик находился на высоте
. В
начальный момент шарик находился на высоте 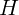 над пружиной. Описать
зависимость координаты шарика от времени. Найти период колебаний.
над пружиной. Описать
зависимость координаты шарика от времени. Найти период колебаний.
1.2.1. Найдите, какое действующее значение тока потребляется в вашем доме, если включены все имеющиеся электрические приборы. Какая при этом энергия выделяется в виде тепла за единицу времени? Рассчитайте средний потребляемый ток по показаниям счетчика электроэнергии.
1.2.2. Две одинаковые электроплитки мощности 1 кВт включаются в электрическую сеть а) параллельно; б) последовательно. Найти суммарную мощность плиток.
 1.2.3. Найти ЭДС, которая возникает на выводах незамкнутой квадратной
проволочной рамки со стороной
1.2.3. Найти ЭДС, которая возникает на выводах незамкнутой квадратной
проволочной рамки со стороной 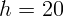 см, которая вращается с частотой
см, которая вращается с частотой
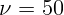 Гц вокруг оси симметрии в постоянном магнитном поле с индукцией
Гц вокруг оси симметрии в постоянном магнитном поле с индукцией
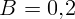 T, направленным перпендикулярно оси вращения. Какая мгновенная и
средняя мощности будут затрачиваться на вращение рамки, если ее выводы
подключить к сопротивлению
T, направленным перпендикулярно оси вращения. Какая мгновенная и
средняя мощности будут затрачиваться на вращение рамки, если ее выводы
подключить к сопротивлению 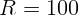 Ом?
Ом?
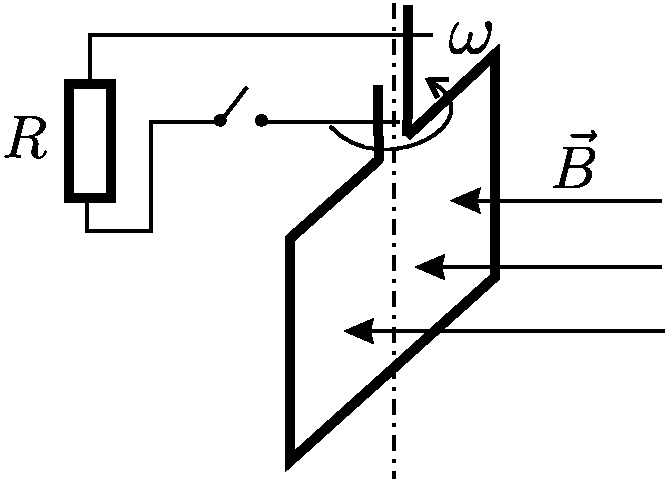
1.2.4. Проводящее кольцо радиуса 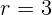 см с сопротивлением
см с сопротивлением 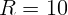 Ом
находится в переменном магнитном поле, направленном перпендикулярно
плоскости кольца и меняющемся по гармоническому закону с амплитудой
Ом
находится в переменном магнитном поле, направленном перпендикулярно
плоскости кольца и меняющемся по гармоническому закону с амплитудой
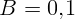 Т и частотой
Т и частотой 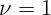 кГц. Найти среднее тепловыделение в кольце.
кГц. Найти среднее тепловыделение в кольце.
1.2.5. В электрическую сеть включается катушка, намотанная медным проводом, с ферромагнитным сердечником и без него. В каком случае катушка нагреется больше?
 1.2.6. В электрическую сеть включен понижающий трансформатор с
коэффициентом трансформации
1.2.6. В электрическую сеть включен понижающий трансформатор с
коэффициентом трансформации 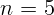 . Ко вторичной обмотке трансформатора
подключен диодный мост, к которому подключена нагрузка. Считая диоды
идеальными, построить график зависимости напряжения на нагрузке от времени.
Найти действующее значение этого напряжения, если действующее напряжение сети
220 В.
. Ко вторичной обмотке трансформатора
подключен диодный мост, к которому подключена нагрузка. Считая диоды
идеальными, построить график зависимости напряжения на нагрузке от времени.
Найти действующее значение этого напряжения, если действующее напряжение сети
220 В.
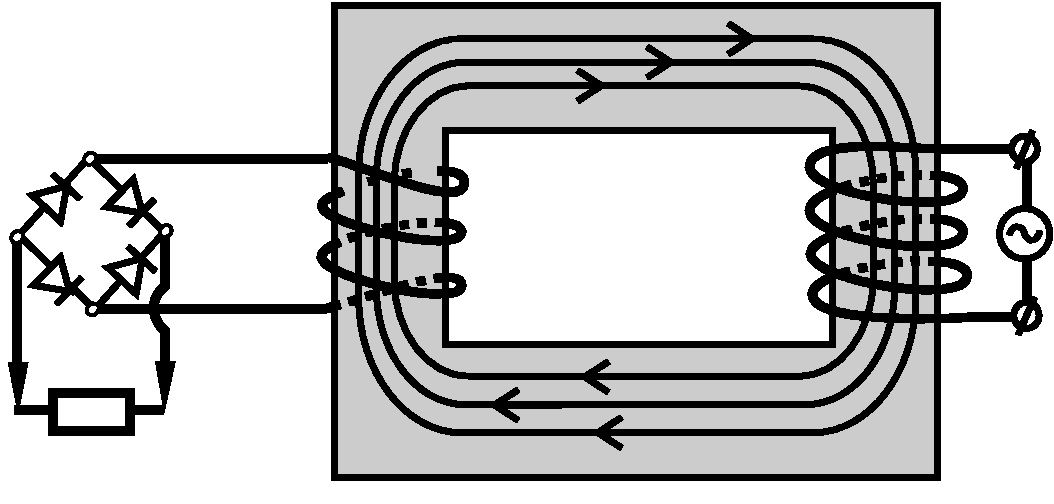
1.2.7. В электрическую сеть переменного тока включены последовательно индуктивность и идеальный диод. Построить качественный график зависимости тока в цепи от времени. Сопротивлением проводов можно пренебречь.
1.2.8. Катушка с индуктивностью 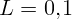 Гн изготовлена из проволоки с
сопротивлением
Гн изготовлена из проволоки с
сопротивлением 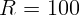 Ом. Чему будет равна амплитуда тока в цепи, если эту
катушку подключить к источнику с действующим значением напряжения
Ом. Чему будет равна амплитуда тока в цепи, если эту
катушку подключить к источнику с действующим значением напряжения
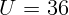 В и частотой
В и частотой 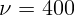 Гц? Найти среднюю мощность тепловыделения в
катушке.
Гц? Найти среднюю мощность тепловыделения в
катушке.
1.2.9. Катушка с индуктивностью 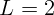 Гн, сопротивления
Гн, сопротивления 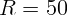 Ом
подключается к источнику ЭДС а) с постоянным напряжением 36 В; б) с
переменным напряжением с частотой 50 Гц и амплитудой 20 В. Найти амплитудное
значение тока в обоих случаях.
Ом
подключается к источнику ЭДС а) с постоянным напряжением 36 В; б) с
переменным напряжением с частотой 50 Гц и амплитудой 20 В. Найти амплитудное
значение тока в обоих случаях.
1.2.10. Конденсатор емкости 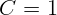 мкФ заряжен до напряжения
мкФ заряжен до напряжения 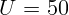 В и
поключается к катушке с индуктивностью
В и
поключается к катушке с индуктивностью 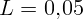 Гн. Сопротивлением проводов
можно пренебречь. Каков будет максимальный ток в цепи?
Гн. Сопротивлением проводов
можно пренебречь. Каков будет максимальный ток в цепи?
1.2.11. Конденсатор какой емкости надо последовательно подсоединить к лампочке, которая расчитана на напряжение 110 В, чтобы ее можно было включить в сеть с действующим напряжением 220 В. Мощность лампочки 55 Вт.
1.3.1. Эхо от выстрела дошло до стрелка через 3 с. На каком расстоянии расположена стена, от которой отразился звук?
1.3.2. Используя справочные данные о модулях Юнга и плотности материалов, найдите скорость звука в стали, в меди и в алюминии.
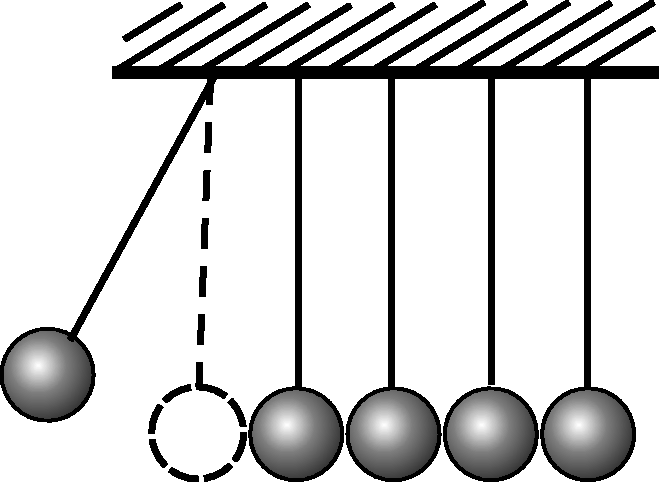
 1.3.3. На штативе висят 5 одинаковых металлических шариков (рис. 3.17).
Между шариками есть небольшой зазор. Крайний левый шарик отклонили на
некоторый угол
1.3.3. На штативе висят 5 одинаковых металлических шариков (рис. 3.17).
Между шариками есть небольшой зазор. Крайний левый шарик отклонили на
некоторый угол 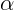 и отпустили. Описать движение шариков, если удары
абсолютно упругие. На какой угол отклонится крайний правый шарик?
и отпустили. Описать движение шариков, если удары
абсолютно упругие. На какой угол отклонится крайний правый шарик?
1.3.4. Найдите частоту звуковых колебаний в воздухе, соответствующую длине волны 10 см, 1 м, 10 м.
1.3.5. Найти частоту ноты "ля" 3-й октавы.
1.3.6. Локомотив двигается со скоростью 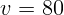 км/ч и издает гудок на
частоте
км/ч и издает гудок на
частоте 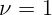 кГц. Гудок какой частоты услышит наблюдатель стоящий перед
поездом? Какую частоту будет слышать наблюдатель, находящийся сзади поезда?
кГц. Гудок какой частоты услышит наблюдатель стоящий перед
поездом? Какую частоту будет слышать наблюдатель, находящийся сзади поезда?
1.3.7. Когда самолет летит с дозвуковой скоростью, на земле слышен шум его двигателей. Если же пролетает сверхзвуковой самолет, то сначала слышен громкий хлопок, а затем уже шум двигателей. С чем это связано?
1.3.8. Стальная пластина со скоростью 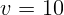 м/с налетает на стальную
стенку. Толщина пластины
м/с налетает на стальную
стенку. Толщина пластины 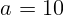 см. Оценить давление, действующее на стенку
во время удара.
см. Оценить давление, действующее на стенку
во время удара.
1.3.9. Найти основную частоту колебаний, которые могут возникнуть между двумя параллельными зданиями, расположенными на расстоянии 20 м.
1.3.10. На двух столбах висят динамики, которые звучат на двух близких частотах. Если встать примерно по середине между столбами, то интенсивность звука меняется от максимальной до нуля и обратно за 2 с. Определите разность звуковых частот динамиков.
1.4.1. Используя табличные данные для показателя преломления найти скорость света в стекле и в воде.
1.4.2. Оценить, за какое время сигнал попадет из Москвы во Владивосток по оптиковолоконной линии и с помощью космической связи. Считать, что скорость света в волокне в 1,5 раза ниже, чем в вакууме.
1.4.3. С помощью шкалы УКВ радиоприемника найдите частоту и длину волны телевизионных каналов, принимаемых в вашем районе.
1.4.4. Определите длину волны зеленого света, которая расположена примерно посередине видимого диапазона оптических волн. Сравните длину волны зеленого света со средним размером атома.
1.4.5. Как энергия излучения заряда, двигающегося по гармоническому закону, зависит от амплитуды и частоты колебаний?
1.4.6. С помощью шкалы вашего радиоприемника измерьте добротность колебательного контура радиоприемника на различных радиодиапазонах.
1.4.7. Две станции работают на длинах волн 10,5 м и 10,7 м. При какой добротности колебательного контура возможно уверенное разделение сигналов этих станций?
2.1.1. Радиус источника света 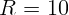 см, а его расстояние до экрана
см, а его расстояние до экрана 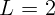 м.
На каком минимальном расстоянии от экрана надо поместить непрозрачный
шар радиуса
м.
На каком минимальном расстоянии от экрана надо поместить непрозрачный
шар радиуса 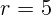 см, чтобы на экране была видна только полутень?
см, чтобы на экране была видна только полутень?
2.1.2. Солнечный свет отражается осколком зеркала на стенку. Оцените
минимальное расстояние до стенки, при котором «солнечный зайчик» будет иметь
вид округлого пятна. Угловой размер Солнца 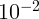 радиан. Поперечный размер
осколка равен примерно 5 см.
радиан. Поперечный размер
осколка равен примерно 5 см.
2.1.3. Зеркало поворачивают на угол 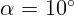 . На какой угол повернется
отраженный световой луч?
. На какой угол повернется
отраженный световой луч?
2.1.4. Чему должен быть равен наименьший размер зеркала, чтобы человек мог видеть самого себя в полный рост?
2.1.5. На какой высоте 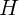 висит уличный фонарь, если тень от вертикально
стоящей палки высотой
висит уличный фонарь, если тень от вертикально
стоящей палки высотой 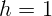 м имеет длину
м имеет длину 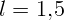 м, а если палку поставить в
конец тени, то новая длина тени
м, а если палку поставить в
конец тени, то новая длина тени 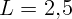 м?
м?
2.1.6. Вертикально стоящий на дне водоема столб высоты 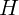 наполовину торчит
из воды, показатель преломления которой равен
наполовину торчит
из воды, показатель преломления которой равен 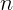 . Найдите длину тени столба
на дне водоема, если угловая высота Солнца над горизонтом равна
. Найдите длину тени столба
на дне водоема, если угловая высота Солнца над горизонтом равна 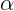 .
.
2.1.7. Водолазу, находящемуся под водой, солнечные лучи кажутся падающими
под углом 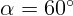 к поверхности воды. Чему равна истинная угловая
высота Солнца над горизонтом? Показатель преломления воды
к поверхности воды. Чему равна истинная угловая
высота Солнца над горизонтом? Показатель преломления воды 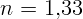 .
.
2.1.8. Под каким углом должен падать световой луч на стекло с показателем
преломления 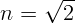 , чтобы угол преломления был в два раза меньше угла
падения?
, чтобы угол преломления был в два раза меньше угла
падения?
2.1.9. Под каким углом должен падать световой луч на стекло, чтобы угол
между отраженным и преломленным лучами был равен 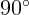 ? Показатель
преломления стекла равен
? Показатель
преломления стекла равен 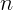 .
.
2.1.10. Показатель преломления стекла относительно воды 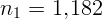 , а
глицерина —
, а
глицерина — 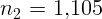 . Найдите показатель преломления стекла относительно
глицерина.
. Найдите показатель преломления стекла относительно
глицерина.
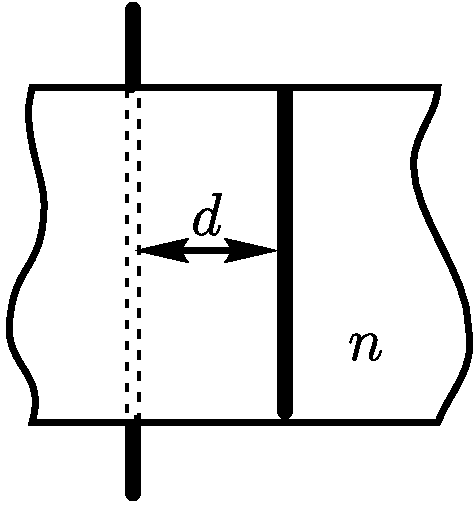
2.1.11. Световой луч падает под углом 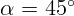 на плоскопараллельную
пластинку из стекла с показателем преломления
на плоскопараллельную
пластинку из стекла с показателем преломления 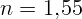 . Найдите величину
смещения луча, если толщина пластинки
. Найдите величину
смещения луча, если толщина пластинки 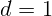 см.
см.
2.1.12. Если смотреть на капиллярную трубку сбоку, то видимый внутренний
диаметр будет равен 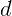 . Чему в действительности равен диаметр капилляра?
Показатель преломления стекла
. Чему в действительности равен диаметр капилляра?
Показатель преломления стекла 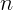 .
.
 2.1.13. Параллельный пучок света падает на плоскую часть стеклянного
полушара радиуса
2.1.13. Параллельный пучок света падает на плоскую часть стеклянного
полушара радиуса 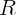 с показателем преломления
с показателем преломления 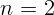 . На каком расстоянии
. На каком расстоянии 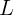 от центра шара надо поставить экран, чтобы радиус светового пятна на экране был
в два раза больше радиуса шара?
от центра шара надо поставить экран, чтобы радиус светового пятна на экране был
в два раза больше радиуса шара?
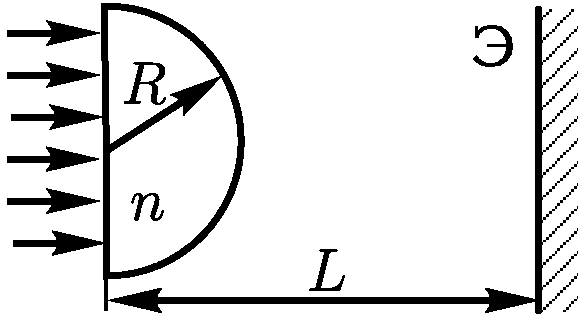
 2.1.14. Точечный источник света
2.1.14. Точечный источник света 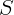 находится внутри стеклянного шара
радиуса
находится внутри стеклянного шара
радиуса 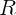 с показателем преломления
с показателем преломления 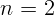 . у дальней поверхности от экрана.
На каком расстоянии
. у дальней поверхности от экрана.
На каком расстоянии 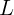 от центра шара надо поставить экран, чтобы радиус
светлого пятна на экране был равен радиусу шара?
от центра шара надо поставить экран, чтобы радиус
светлого пятна на экране был равен радиусу шара?
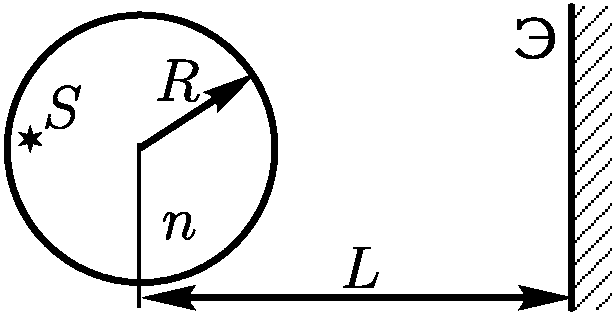
2.1.15. Точечный источник света перемещается от центра сферического зеркала к его фокусу. Как перемещается при этом изображение источника?
2.1.16. Изображение предмета в сферическом зеркале в три раза меньше самого предмета. Если предмет придвинуть к зеркалу на 15 см, то изображение станет в 1,5 раза меньше предмета. Найдите фокусное расстояние зеркала.
2.1.17. Радиус кривизны вогнутого зеркала 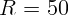 см. На каком расстоянии
от полюса зеркала надо поместить предмет, чтобы его изображение было
действительным и увеличенным в 2 раза?
см. На каком расстоянии
от полюса зеркала надо поместить предмет, чтобы его изображение было
действительным и увеличенным в 2 раза?
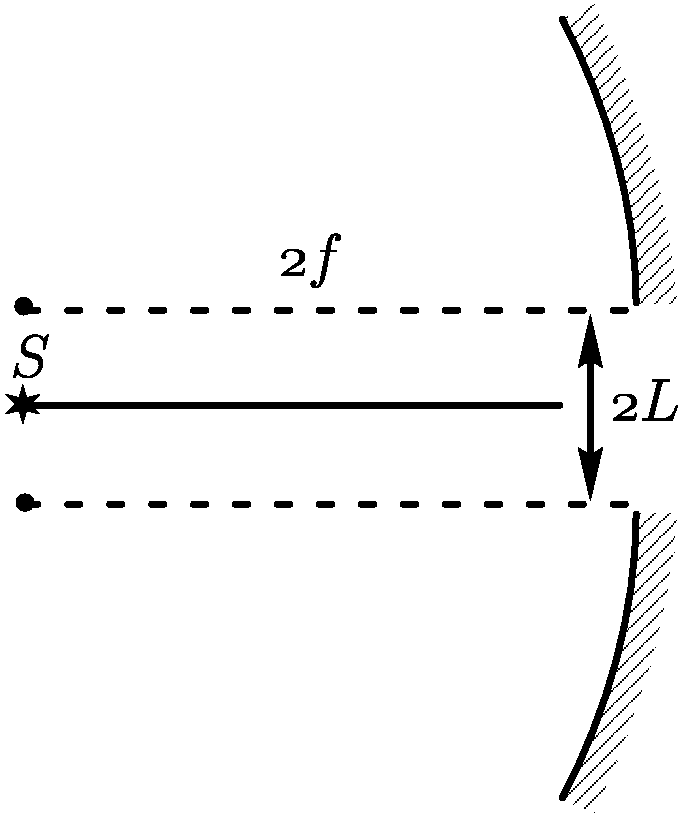
 2.1.18. Точечный источник света установлен в центре сферического зеркала с
фокусным расстоянием
2.1.18. Точечный источник света установлен в центре сферического зеркала с
фокусным расстоянием 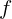 . Зеркало разрезали на две половинки и отодвинули
каждую на расстояние
. Зеркало разрезали на две половинки и отодвинули
каждую на расстояние 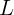 от главной оптической оси, не меняя их взаимной
ориентации. Чему равно расстояние между изображениями в двух половинках
зеркала?
от главной оптической оси, не меняя их взаимной
ориентации. Чему равно расстояние между изображениями в двух половинках
зеркала?
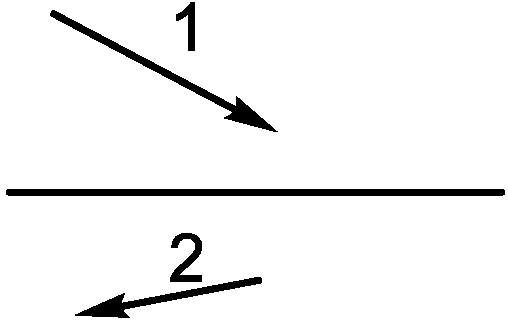
 2.1.19. Дан ход светового луча до (1) и после (2) отражения в сферическом
зеркале. Геометрическим построением найдите положение фокуса и центра зеркала.
Направление главной оптической оси изображено на рисунке.
2.1.19. Дан ход светового луча до (1) и после (2) отражения в сферическом
зеркале. Геометрическим построением найдите положение фокуса и центра зеркала.
Направление главной оптической оси изображено на рисунке.
2.1.20. На каком расстоянии от полюса сферического зеркала с фокусным
расстоянием 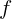 надо поместить точечный источник света на главной оптической
оси, чтобы положение источника совпало с его изображением, если поставить
плоское зеркало на расстоянии
надо поместить точечный источник света на главной оптической
оси, чтобы положение источника совпало с его изображением, если поставить
плоское зеркало на расстоянии 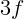 перпендикулярно главной оптической оси?
перпендикулярно главной оптической оси?
 2.1.21. Человек смотрит на вертикально висящую проволоку, часть которой
прикрыта стеклянным клином с малым углом при вершине. Вид проволоки в клине
смещен относительно ее прямого вида на расстояние
2.1.21. Человек смотрит на вертикально висящую проволоку, часть которой
прикрыта стеклянным клином с малым углом при вершине. Вид проволоки в клине
смещен относительно ее прямого вида на расстояние 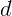 . На каком удалении
. На каком удалении 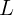 от
клина висит проволока? Показатель преломления стекла равен
от
клина висит проволока? Показатель преломления стекла равен 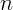 . Боковые
плоскости клина параллельны проволоке.
. Боковые
плоскости клина параллельны проволоке.
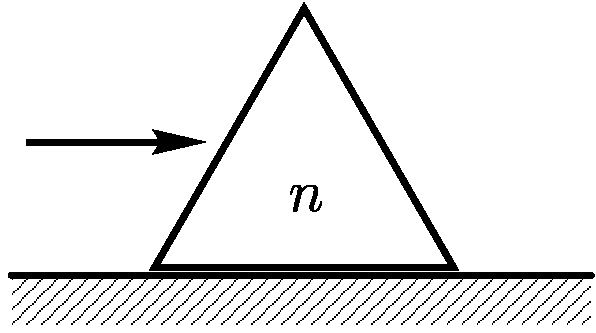
 2.1.22. На стеклянную призму, представляющую в сечении равносторонний
треугольник, параллельно основанию падает световой луч. При каком минимальном
показателе преломления стекла луч не выйдет через вторую боковую грань?
2.1.22. На стеклянную призму, представляющую в сечении равносторонний
треугольник, параллельно основанию падает световой луч. При каком минимальном
показателе преломления стекла луч не выйдет через вторую боковую грань?
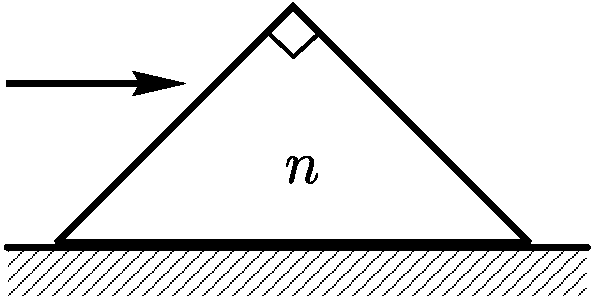
 2.1.23. На равнобедренную призму с прямым углом при вершине параллельно
основанию падает световой луч. Чему равен показатель преломления стекла
2.1.23. На равнобедренную призму с прямым углом при вершине параллельно
основанию падает световой луч. Чему равен показатель преломления стекла 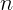 ,
если луч испытывает полное внутреннее отражение у основания призмы?
,
если луч испытывает полное внутреннее отражение у основания призмы?
2.1.24. Свеча находится на расстоянии 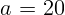 см от собирающей линзы,
фокусное расстояние которой
см от собирающей линзы,
фокусное расстояние которой 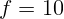 см. На каком расстоянии от линзы будет
находиться изображение свечи?
см. На каком расстоянии от линзы будет
находиться изображение свечи?
2.1.25. На каком расстоянии 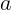 от линзы надо поместить предмет, чтобы
поперечный размер его действительного изображения был в три раза больше самого
предмета? Фокусное расстояние линзы
от линзы надо поместить предмет, чтобы
поперечный размер его действительного изображения был в три раза больше самого
предмета? Фокусное расстояние линзы 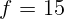 см.
см.
2.1.26. Определите фокусное расстояние рассеивающей линзы, если известно, что предмет, помещенный перед ней на расстоянии 40 см дает мнимое изображение, уменьшенное в четыре раза.
2.1.27. Расстояние от предмета до экрана 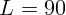 см. Где надо поставить между
ними линзу с фокусным расстоянием
см. Где надо поставить между
ними линзу с фокусным расстоянием 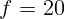 см, чтобы получить на экране четкое
изображение предмета?
см, чтобы получить на экране четкое
изображение предмета?
2.1.28. Расстояние от предмета до экрана 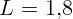 м. Линзу с каким фокусным
расстоянием надо взять и где следует ее поставить, чтобы получить изображение
предмета, увеличенное в два раза?
м. Линзу с каким фокусным
расстоянием надо взять и где следует ее поставить, чтобы получить изображение
предмета, увеличенное в два раза?
2.1.29. Четкое изображение лампы на экране возникает при двух положениях
линзы, отстоящих на расстоянии 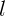 . Найдите фокусное расстояние линзы, если
расстояние между лампой и экраном равно
. Найдите фокусное расстояние линзы, если
расстояние между лампой и экраном равно 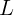 .
.
 2.1.30. Точечный источник света
2.1.30. Точечный источник света 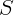 перемещают параллельно главной
оптической оси линзы на расстоянии
перемещают параллельно главной
оптической оси линзы на расстоянии 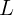 от нее. Под каким углом к оси будет
двигаться изображение, если фокусное расстояние линзы
от нее. Под каким углом к оси будет
двигаться изображение, если фокусное расстояние линзы 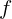 ?
?
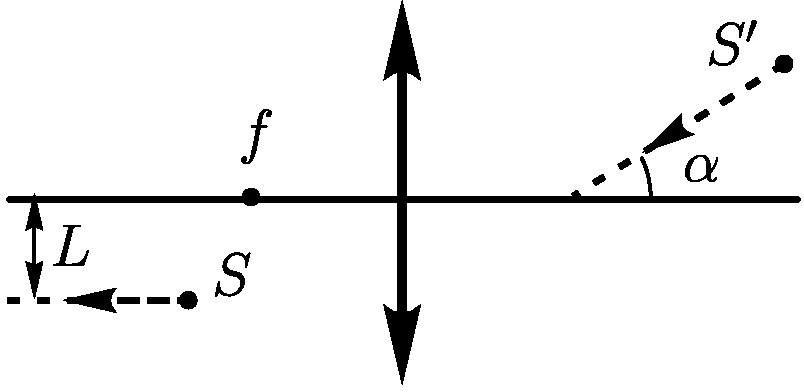
2.1.31. Две линзы с фокусными расстояниями 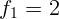 см и
см и 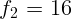 см, стоят на
расстоянии
см, стоят на
расстоянии 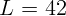 см друг от друга так, что их оптические оси совпадают.
Предмет находится на расстоянии
см друг от друга так, что их оптические оси совпадают.
Предмет находится на расстоянии 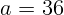 см слева от первой линзы. На
каком расстоянии справа от второй линзы будет изображение предмета?
см слева от первой линзы. На
каком расстоянии справа от второй линзы будет изображение предмета?
 2.1.32. Даны положения оптического центра линзы и ход произвольного
светового луча через линзу. Найдите геометрическим построением положения
главных фокусов линзы и направление главной оптической оси.
2.1.32. Даны положения оптического центра линзы и ход произвольного
светового луча через линзу. Найдите геометрическим построением положения
главных фокусов линзы и направление главной оптической оси.
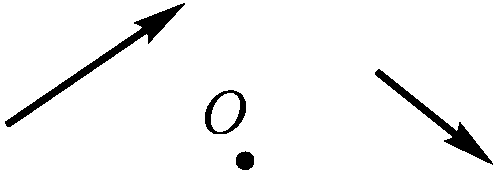
2.1.33. Если 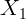 — расстояние от предмета до переднего фокуса линзы, а
— расстояние от предмета до переднего фокуса линзы, а
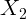 — от заднего фокуса до изображения, то имеет место соотношение:
— от заднего фокуса до изображения, то имеет место соотношение:
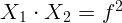 (формула Ньютона), где
(формула Ньютона), где 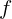 — фокусное расстояние линзы. Докажите
справедливость этой формулы.
— фокусное расстояние линзы. Докажите
справедливость этой формулы.
2.1.34. Две тонкие линзы с фокусными расстояниями 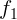 и
и 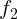 стоят вплотную
одна к другой. Найдите, чему равно фокусное расстояние такой системы.
стоят вплотную
одна к другой. Найдите, чему равно фокусное расстояние такой системы.
2.1.35. Две линзы стоят на расстоянии 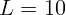 см друг от друга. Фокусные
расстояния линз
см друг от друга. Фокусные
расстояния линз 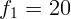 см и
см и 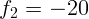 см. На каком расстоянии от второй линзы
сфокусируется параллельный световой пучок?
см. На каком расстоянии от второй линзы
сфокусируется параллельный световой пучок?
2.1.36. Объектив фотоаппарата имеет фокусное расстояние 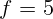 см. На каком
расстоянии от объектива должен находиться предмет, чтобы снимок получился в
1:20 натуральной величины?
см. На каком
расстоянии от объектива должен находиться предмет, чтобы снимок получился в
1:20 натуральной величины?
2.1.37. Делают снимок телебашни высотой 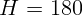 м. Размер фотокадра на
пленке
м. Размер фотокадра на
пленке 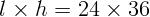 мм. На каком наименьшем расстоянии надо встать
фотографу, чтобы вся башня по высоте уместилась на пленке, если фокусное
расстояние фотоаппарата
мм. На каком наименьшем расстоянии надо встать
фотографу, чтобы вся башня по высоте уместилась на пленке, если фокусное
расстояние фотоаппарата 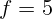 см ?
см ?
2.1.38. Требуется сделать фотографию бегуна, скорость которого 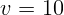 м/с.
Определите максимально допустимое время экспозиции, чтобы размытость
изображения на пленке не превышала
м/с.
Определите максимально допустимое время экспозиции, чтобы размытость
изображения на пленке не превышала 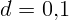 мм. Фокусное расстояние объектива
мм. Фокусное расстояние объектива
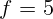 см, а расстояние до бегуна
см, а расстояние до бегуна 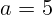 м.
м.
2.1.39. Предмет, сфотографированный с расстояния 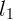 , получился на
пленке высотой
, получился на
пленке высотой 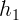 , а при фотографировании с расстояния
, а при фотографировании с расстояния 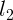 высота
изображения
высота
изображения 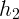 . Найдите фокусное расстояние объектива фотоаппарата.
. Найдите фокусное расстояние объектива фотоаппарата.
2.1.40. Чему равно фокусное расстояние объектива проекционного аппарата, если на экране получается стократное увеличение? Расстояние до экрана равно 4 м.
2.1.41. Фокусное расстояние объектива проекционного аппарата равно 20 см. На
каком расстоянии от объектива надо поставить диапозитив с размером кадра
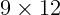 см, чтобы его изображение точно уместилось на экране с размерами
см, чтобы его изображение точно уместилось на экране с размерами
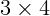 м?
м?
2.1.42. Оптическая сила очковых линз равна 1 дптр. Чему равно фокусное расстояние линз?
2.1.43. Оцените, с какого расстояния от наблюдателя в ясную погоду железнодорожные рельсы сольются в одну линию.
2.1.44. На каком расстоянии от лица надо держать зеркало, чтобы рассматривать в нем мелкие черты лица?
2.1.45. Определите фокусное расстояние лупы, дающей пятикратное увеличение.
2.1.46. В качестве лупы используется очковая линза с оптической силой 8 дптр. Какое увеличение можно получить с помощью такой лупы?
2.1.47. Увеличение микроскопа 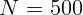 . Определите фокусное расстояние
объектива, если фокусное расстояние окуляра
. Определите фокусное расстояние
объектива, если фокусное расстояние окуляра 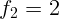 см, а длина тубуса
см, а длина тубуса 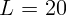 см.
см.
2.1.48. Фокусное расстояние объектива микроскопа 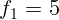 мм, а окуляра
мм, а окуляра
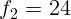 мм. Увеличение микроскопа
мм. Увеличение микроскопа 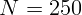 . Чему равно расстояние между
фокусами объектива и окуляра?
. Чему равно расстояние между
фокусами объектива и окуляра?
2.1.49. Фокусное расстояние объектива зрительной трубы 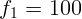 см, окуляра
см, окуляра
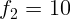 см. Под каким углом
см. Под каким углом 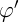 будет виден диаметр лунного диска, если
угловой диаметр Луны при наблюдении невооруженным глазом
будет виден диаметр лунного диска, если
угловой диаметр Луны при наблюдении невооруженным глазом 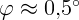 ?
?
2.1.50. Зрительная труба имеет пятидесятикратное увеличение. Фокусное
расстояние объектива 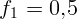 м. Чему равны фокусное расстояние окуляра и
полная длина зрительной трубы?
м. Чему равны фокусное расстояние окуляра и
полная длина зрительной трубы?
2.2.1. Сколько времени идет свет от Солнца до Земли?
2.2.2. В 1875 г. метод измерения скорости света Физо был использован
французским физиком Корню. Число зубцов в колесе было равно 200. При частоте
вращения колеса 914,3 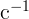 наблюдалось 28 появлений света. Какое значение для
скорости света получил Корню, если расстояние от зубчатого колеса до зеркала
было равно 23 км?
наблюдалось 28 появлений света. Какое значение для
скорости света получил Корню, если расстояние от зубчатого колеса до зеркала
было равно 23 км?
2.2.3. Длина волны света в стекле 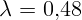 мкм при частоте
мкм при частоте 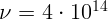 Гц.
Чему равна скорость света в стекле?
Гц.
Чему равна скорость света в стекле?
2.2.4. На отрезке длиной 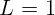 см укладывается
см укладывается 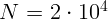 длин волн с
частотой
длин волн с
частотой 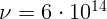 Гц. Чему равна скорость волны?
Гц. Чему равна скорость волны?
 2.2.5. Между двумя стеклянными пластинками длиной 20 см с одного края
зажата проволока диаметром 20 мкм. Какой вид будет иметь интерференционная
картина? Сколько интерференционных полос уложится вдоль пластинки, если она
освещается светом с длиной волны 500 нм? Чему равно расстояние между двумя
соседними полосами?
2.2.5. Между двумя стеклянными пластинками длиной 20 см с одного края
зажата проволока диаметром 20 мкм. Какой вид будет иметь интерференционная
картина? Сколько интерференционных полос уложится вдоль пластинки, если она
освещается светом с длиной волны 500 нм? Чему равно расстояние между двумя
соседними полосами?
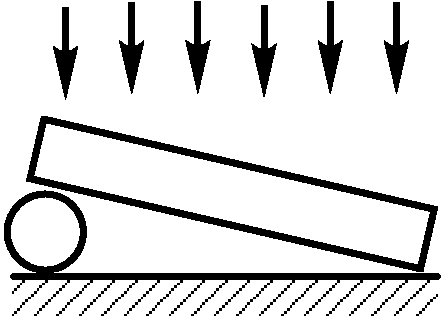
 2.2.6. Два одинаковых плоских зеркала образуют между собой тупой угол
2.2.6. Два одинаковых плоских зеркала образуют между собой тупой угол
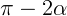
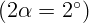 . Точечный источник света находится на биссектрисе угла на
расстоянии 10 см от зеркал (рис. 6.18). Найти расстояние между светлыми
полосами на экране, если длина волны света равна 650 нм. Экран удален на 8 м от
точки пересечения зеркал. Прямые лучи света от источника на экран не
попадают.
. Точечный источник света находится на биссектрисе угла на
расстоянии 10 см от зеркал (рис. 6.18). Найти расстояние между светлыми
полосами на экране, если длина волны света равна 650 нм. Экран удален на 8 м от
точки пересечения зеркал. Прямые лучи света от источника на экран не
попадают.
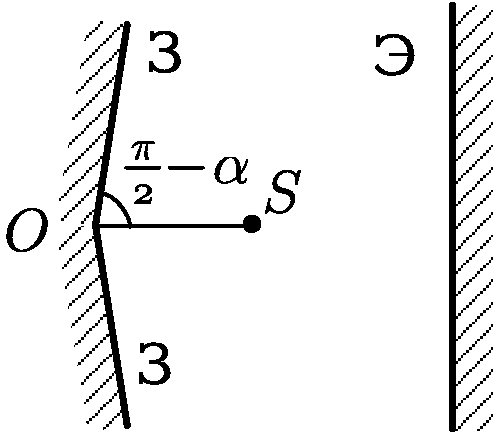
2.2.7. Из собирающей линзы диаметра 5 см и с фокусным расстоянием 50 см симметрично относительно центра вырезана полоса шириной 1 см. Оставшиеся части линзы сдвинуты вплотную. На каком расстоянии от линзы еще можно наблюдать интерференционную картину, если точечный источник света удален от линзы на 75 см? На каком расстоянии от линзы ширина интерференционной картины на экране будет максимальна? Для этого положения экрана найти расстояние между интерференционными полосами, если длина волны света равна 500 нм.
2.2.8. Два когерентных источника света  и
и  освещают экран, плоскость
которого параллельна линии
освещают экран, плоскость
которого параллельна линии 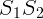 . Чему равна длина волны света, если
расстояние между двумя соседними максимумами освещенности на экране равно
1,2 мм? Расстояние до экрана равно 4,8 м, а между источниками света — 2 мм.
. Чему равна длина волны света, если
расстояние между двумя соседними максимумами освещенности на экране равно
1,2 мм? Расстояние до экрана равно 4,8 м, а между источниками света — 2 мм.
 2.2.9. Точечный источник света расположен на расстоянии 20 см от
левого края плоского зеркала, длина которого также равна 20 см. Высота
источника над плоскостью зеркала равна 1 см. Найти вертикальный размер
интерференционной картины на экране, удаленном на расстояние 5 м. Найти
расстояние между двумя соседними максимумами освещенности, если длина
волны света равна 0,6 мкм. Оцените число интерференционных полос на
экране.
2.2.9. Точечный источник света расположен на расстоянии 20 см от
левого края плоского зеркала, длина которого также равна 20 см. Высота
источника над плоскостью зеркала равна 1 см. Найти вертикальный размер
интерференционной картины на экране, удаленном на расстояние 5 м. Найти
расстояние между двумя соседними максимумами освещенности, если длина
волны света равна 0,6 мкм. Оцените число интерференционных полос на
экране.
 2.2.10. Два точечных монохроматических источника света
2.2.10. Два точечных монохроматических источника света  и
и  расположены на расстоянии
расположены на расстоянии 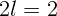 мм друг от друга. На экране, удаленном на
10 м от первого источника в точке
мм друг от друга. На экране, удаленном на
10 м от первого источника в точке 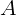 наблюдается максимум интерференции.
Если источник света
наблюдается максимум интерференции.
Если источник света 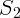 отодвинуть от первого, то при некотором смещении в
точке
отодвинуть от первого, то при некотором смещении в
точке 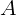 наступает потемнение. Найдите это минимальное смещение, если длина
волны света равна 600 нм.
наступает потемнение. Найдите это минимальное смещение, если длина
волны света равна 600 нм.
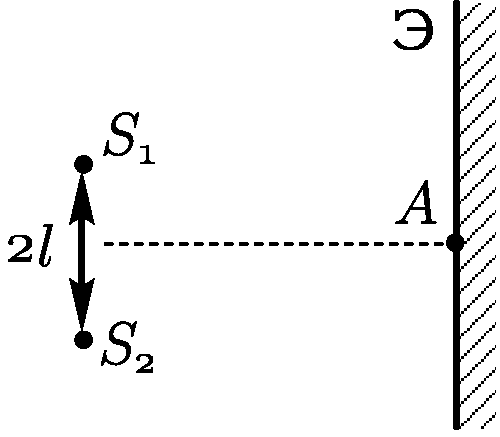
 2.2.11. Точечный источник света расположен на расстоянии 2 м от
экрана. Слева от источника на расстоянии 1 см стоит плоское зеркало,
параллельное экрану. На экране наблюдается интерференционная картина в виде
концентрических колец. Найти длину волны света, если радиус светлого пятна в
центре равен 1 см. Докажите, что площадь любого светлого кольца не зависит от
его номера.
2.2.11. Точечный источник света расположен на расстоянии 2 м от
экрана. Слева от источника на расстоянии 1 см стоит плоское зеркало,
параллельное экрану. На экране наблюдается интерференционная картина в виде
концентрических колец. Найти длину волны света, если радиус светлого пятна в
центре равен 1 см. Докажите, что площадь любого светлого кольца не зависит от
его номера.
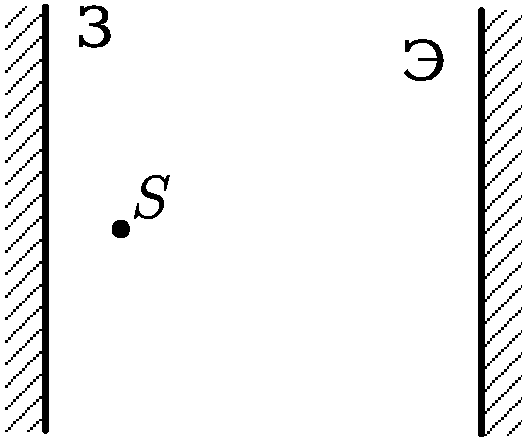
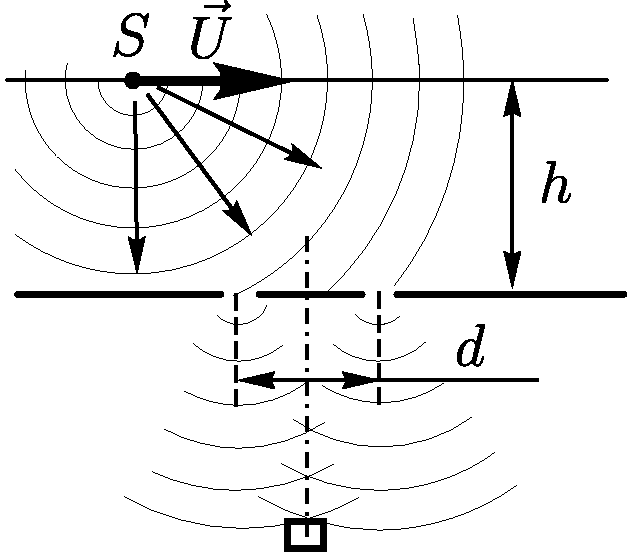
 2.2.12. Точечный источник света равномерно движется на удалении
2.2.12. Точечный источник света равномерно движется на удалении 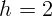 м
от плоскости, в которой имеются два маленьких отверстия на расстоянии
м
от плоскости, в которой имеются два маленьких отверстия на расстоянии
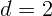 мм друг от друга. Приемник света
мм друг от друга. Приемник света 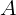 , расположенный симметрично
относительно отверстий, регистрирует периодически меняющуюся интенсивность
света с частотой 10 Гц. Определить скорость источника
, расположенный симметрично
относительно отверстий, регистрирует периодически меняющуюся интенсивность
света с частотой 10 Гц. Определить скорость источника 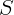 , если длина волны
света
, если длина волны
света 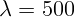 нм.
нм.
2.2.13. Для измерения колец Ньютона используется плоско-выпуклая линза с радиусом кривизны 10 м. Определить длину волны зеленой линии ртутной лампы, если второе светлое кольцо имеет радиус 1,66 мм.
2.2.14. Чему равен радиус кривизны линзы в опыте Ньютона, если для красного света с длиной волны 650 нм радиус пятого светлого кольца равен 2 мм?
2.2.15. В опыте Ньютона линза освещается красным (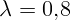 мкм) и
фиолетовым (
мкм) и
фиолетовым (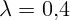 мкм) светом. Расстояние между первым красным и
вторым фиолетовым кольцами равно 0,59 мм. Найти радиус кривизны линзы.
мкм) светом. Расстояние между первым красным и
вторым фиолетовым кольцами равно 0,59 мм. Найти радиус кривизны линзы.
2.2.16. Дифракционная решетка содержит 100 штрихов на 1 мм. Найти длину
волны света, падающего на решетку, если угол между максимумами первого
порядка равен 6 .
.
2.2.17. Расстояние на экране между максимумами первого порядка для красного
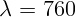 нм и фиолетового
нм и фиолетового 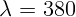 нм света равно 3,8 см. Чему равен период
решетки, если расстояние до экрана равно 1 м?
нм света равно 3,8 см. Чему равен период
решетки, если расстояние до экрана равно 1 м?
2.2.18. Оцените, сколько штрихов на 1 мм должна иметь дифракционная решетка, пригодная для исследования инфракрасных лучей с длиной волны около 100 мкм?
2.2.19. Главный дифракционный максимум второго порядка для света с длиной волны 0,6 мкм совпадает с главным дифракционным максимумом третьего порядка для фиолетового света. Найти длину волны фиолетового света.
2.2.20. Оцените, чему должен быть равен диаметр выходного окна рубинового
лазера (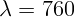 нм), чтобы на экране, удаленном на расстоянии 10 м, получилось
световое пятно минимального размера.
нм), чтобы на экране, удаленном на расстоянии 10 м, получилось
световое пятно минимального размера.
2.3.1. Свет, отраженный от поверхности воды, частично поляризован. Как можно убедиться в этом, имея поляроид?
2.3.2. Интенсивность света после второго поляроида уменьшилась в четыре раза. Чему равен угол между осями поляроидов?
2.3.3. Угол между двумя осями поляроидов равен 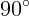 . Третий поляроид
установлен между ними так, что его ось составляет угол
. Третий поляроид
установлен между ними так, что его ось составляет угол 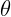 с осью первого
поляроида. Во сколько раз ослабнет энергия прошедшего светового пучка?
с осью первого
поляроида. Во сколько раз ослабнет энергия прошедшего светового пучка?
2.3.4. На зеленой бумаге написан текст красными буквами. Через стекло какого цвета будет видна надпись?
2.3.5. Длина волны красного света в воде равна длине волны зеленого света в воздухе. Вода освещается зеленым светом. Какой цвет будет видеть человек, находящийся под водой?
2.3.6. Какого цвета будет окраска, если смешать лучи желтого и зеленого цвета? Голубого и зеленого?
2.3.7. Оцените радиус черной дыры, если ее масса в миллион раз больше массы
Солнца. Масса Солнца 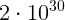 кг.
кг.
2.4.1. Световой поток 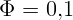 лм падает равномерно и перпендикулярно на
площадку
лм падает равномерно и перпендикулярно на
площадку 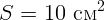 . Чему равна ее освещенность?
. Чему равна ее освещенность?
2.4.2. Лампа, сила света которой 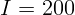 кд, висит над землей на высоте
кд, висит над землей на высоте
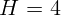 м. Найдите освещенность площадки на земле непосредственно под лампой
и на расстоянии
м. Найдите освещенность площадки на земле непосредственно под лампой
и на расстоянии 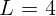 м от этой точки.
м от этой точки.
2.4.3. Сила света светлячка 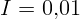 кд. Сколько надо взять светлячков,
чтобы на расстоянии
кд. Сколько надо взять светлячков,
чтобы на расстоянии 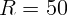 см освещенность была такая же, как и от полной
Луны (
см освещенность была такая же, как и от полной
Луны (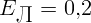 лк)?
лк)?
2.4.4. Лампу, с силой света 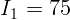 кд, заменили лампой с силой света
кд, заменили лампой с силой света
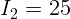 кд и приблизили к освещаемой поверхности, уменьшив расстояние в три
раза. Во сколько раз изменилась освещенность поверхности?
кд и приблизили к освещаемой поверхности, уменьшив расстояние в три
раза. Во сколько раз изменилась освещенность поверхности?
2.4.5. Найдите наибольшее расстояние, с которого ночью можно увидеть лампу с
силой света 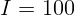 кд, если порог чувствительности глаза
кд, если порог чувствительности глаза 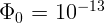 лм.
Площадь зрачка глаза в темноте
лм.
Площадь зрачка глаза в темноте 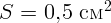 .
.
2.4.6. Источник света, создает в центре экрана освещенность 2 лк. Насколько изменится освещенность экрана, если по другую сторону от источника поставить плоское зеркало на расстоянии, равном половине расстояния источника до экрана?
2.4.7. Лампа, сила света которой 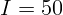 кд, висит над землей на высоте
кд, висит над землей на высоте
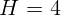 м. Под лампой установили горизонтально линзу так, чтобы она находилась
в ее фокусе. Во сколько раз повысилась освещенность непосредственно под
лампой после установки линзы? Фокусное расстояние линзы
м. Под лампой установили горизонтально линзу так, чтобы она находилась
в ее фокусе. Во сколько раз повысилась освещенность непосредственно под
лампой после установки линзы? Фокусное расстояние линзы 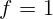 м.
м.
2.4.8. В ясную ночь Луна создает освещенность 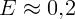 лк при угле над
горизонтом
лк при угле над
горизонтом 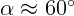 . Чему равна поверхностная яркость Луны? Радиус Луны
. Чему равна поверхностная яркость Луны? Радиус Луны
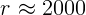 км, а расстояние до Земли
км, а расстояние до Земли 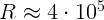 км.
км.
2.4.9. В фокусе сферического зеркального прожектора расположена ртутная лампа. Колба лампы имеет матовую поверхность и сферическую форму конечных размеров. Оцените освещенность на расстоянии 1 км от прожектора, если поверхностная яркость лампы 10 нт. Поперечный диаметр зеркала равен 0,5 м. Считать, что фокусное расстояние зеркала много больше радиуса колбы лампы.
2.4.10. Оцените поверхностную яркость Солнца, если освещенность Земли в
ясную погоду равна примерно 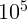 лк. Угловой размер Солнца равен
лк. Угловой размер Солнца равен 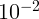 радиан.
радиан.
3.1.1. Космонавтам предстоит лететь к звезде, удаленной на расстояние 20 световых лет. С какой скоростью необходимо лететь, чтобы полет в оба конца занял 10 лет по корабельным часам? Сколько времени при этом пройдет на Земле?
3.1.2. При какой скорости частицы ее полная энергия вдвое превосходит энергию покоя?
3.1.3. Какую работу нужно совершить, чтобы разогнать протон до скорости
0,999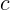 ?
?
3.1.4. С какой минимальной энергией должны двигаться навстречу друг другу два протона, чтобы при столкновении могли родиться дополнительный протон и антипротон?
3.1.5. Две частицы, каждая массой 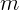 , летят со скоростями
, летят со скоростями 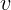 навстречу друг
другу и при столкновении слипаются. Чему равна масса новой частицы?
навстречу друг
другу и при столкновении слипаются. Чему равна масса новой частицы?
3.1.6. В хвосте релятивистского поезда произошел взрыв, и через время 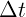 его
увидели наблюдатели, находящиеся в голове поезда. Какое время пройдет между
этими двумя событиями в системе Земли, если скорость поезда равна 0,6
его
увидели наблюдатели, находящиеся в голове поезда. Какое время пройдет между
этими двумя событиями в системе Земли, если скорость поезда равна 0,6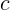 ?
?
3.1.7. Под каким углом к горизонту виден светящийся предмет, движущийся
горизонтально со скоростью 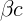 в момент, когда находится над наблюдателем?
в момент, когда находится над наблюдателем?
 3.1.8. Стеклянный брусок длины
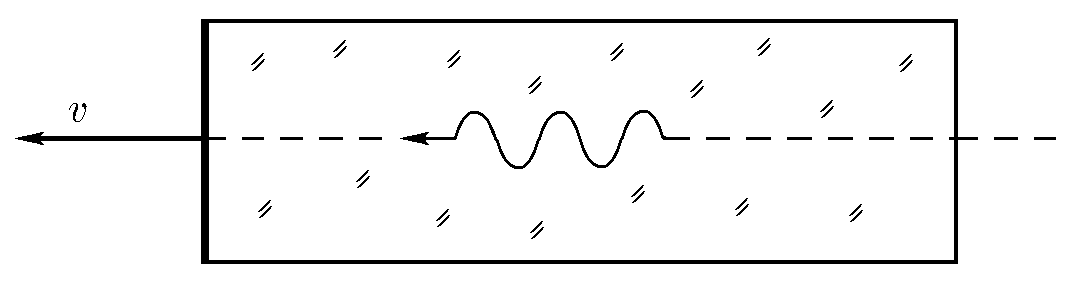
3.1.8. Стеклянный брусок длины 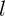 движется в продольном направлении со
скоростью
движется в продольном направлении со
скоростью 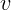 . Передний торец бруска посеребрен. Сколько времени по часам
неподвижного наблюдателя потребуется свету, входящему в брусок через задний
торец, чтобы пройти по бруску, отразиться от посеребренного торца и выйти из
бруска? Коэффициент преломления стекла
. Передний торец бруска посеребрен. Сколько времени по часам
неподвижного наблюдателя потребуется свету, входящему в брусок через задний
торец, чтобы пройти по бруску, отразиться от посеребренного торца и выйти из
бруска? Коэффициент преломления стекла 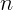 .
.
4.1.1. Оценить, какую разность потенциалов должны пройти электроны, чтобы
длина волны де Бройля этих электронов была равна длине волны красного света
(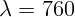 нм).
нм).
4.1.2. Чему равна длина волны де Бройля протонов с энергией 1 ТэВ? Какого размера объекты можно рассмотреть с помощью "микроскопа", в котором вместо света используются протоны такой энергии?
4.1.3. Какую нужно затратить работу, чтобы оторвать электрон от иона гелия с
одним электроном (He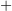 )?
)?
4.1.4. Каким бы был размер атома, если бы электрон притягивался к протону только за счет гравитационных сил? Сравнить с размером видимой части Вселенной (10 млрд. св. лет).
4.1.5. Импульс лазера имеет длину волны 500 нм и длительность 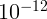 с.
Оценить степень монохроматичности излучения
с.
Оценить степень монохроматичности излучения 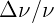 , воспользовавшись
соотношением неопределеностей Гейзенберга.
, воспользовавшись
соотношением неопределеностей Гейзенберга.
4.2.1. Какой элемент образуется при 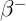 -распаде
-распаде 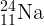 , при
, при 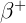 -распаде
-распаде
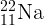 ?
?
4.2.2. Впишите недостающие частицы в распадах 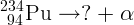 ,
,
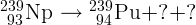 .
.
4.2.3. Кусок ископаемого дерева, содержащий 100 г углерода, испускает в
среднем одну 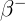 -частицу в секунду. Определить возраст образца, если известно,
что в живых деревьях отношение количества изотопов углерода
-частицу в секунду. Определить возраст образца, если известно,
что в живых деревьях отношение количества изотопов углерода 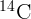 к
к
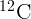 составляет
составляет 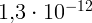 , а период полураспада
, а период полураспада 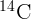 равен 5730 лет?
равен 5730 лет?
4.2.4. Во сколько раз изменится критическая масса урана, если его превратить в стружку с плотностью в 2 раза меньше, чем у исходного материала?
4.2.5. Поток энергии от Солнца на Землю составляет 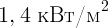 . Однако за
счет различных факторов можно использовать только 3% приходящей энергии.
Найдите площадь, которую нужно покрыть приемниками света, чтобы производить
5 ГВт электрической энергии (характерная мощность электростанции).
. Однако за
счет различных факторов можно использовать только 3% приходящей энергии.
Найдите площадь, которую нужно покрыть приемниками света, чтобы производить
5 ГВт электрической энергии (характерная мощность электростанции).
4.2.6. Доза облучения, получаемая человеком от всех источников, составляет около 10 мкбэр/час. Какую долю составляют космические частицы в этой дозе, если за год они дают 0,05 бэр?
4.3.1. До какой энергии можно ускорить протоны в кольце радиусом 10 км, если поворотные магниты имеют предельное поле 10 Tл?
4.3.2. Какие из перечисленных ниже распадов противоречат законам сохранения и каким?
4.3.3. Масса нейтрального пиона равна 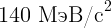 . Покоящийся пион
распадается на два фотона. Найти энергии фотонов.
. Покоящийся пион
распадается на два фотона. Найти энергии фотонов.
4.3.4. Допишите реакцию, в которой при электрон–позитронной аннигиляции
рождаются два заряженных пиона: 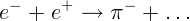 .
.
1.1.1. 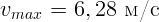 ,
, 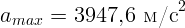 .
.
1.1.2. 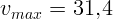 м/с,
м/с, 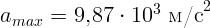 ,
, 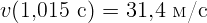 ,
,
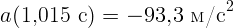 .
.
1.1.3. Путь: 20 мкм, 1,9 мм, 2 см, 4 см, 8 см; Перемещение: 20 мкм, 1,9 мм, 2 см, 0 см, 0 см.
1.1.4. 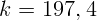 Н/м.
Н/м.
1.1.5. 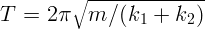 .
.
1.1.6. 20 с.
1.1.7. Будут отставать в 2,4 раза.
1.1.8. 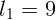 см,
см, 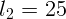 см.
см.
1.1.9. Свободно падающий шарик.
1.1.10. 3,7 мДж.
1.1.11. 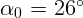 ,
, 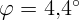 .
.
1.1.12. 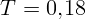 с,
с, 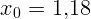 см,
см, 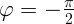 ,
, 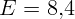 мДж; период не изменится,
мДж; период не изменится,
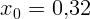 мм,
мм, 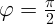 ,
, 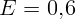 мДж.
мДж.
1.1.13. 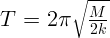 .
.
1.1.14. 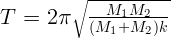 .
.
1.1.15. 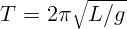 .
.
1.1.16. 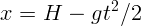 при
при 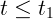 ,
, 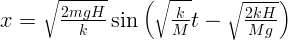 при
при 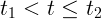 ,
,
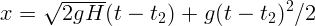 при
при 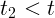 ;
; 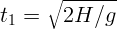 ,
, 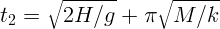 .
.
1.2.1.
1.2.2. 0,5 кВт.
1.2.3. 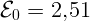 В,
В, 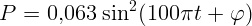 ,
, 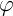 — произвольная константа,
— произвольная константа,
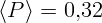 кВт.
кВт.
1.2.4.
1.2.5. Нагрев одинаков.
1.2.6. 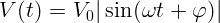 ,
, 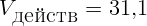 В.
В.
1.2.7.
1.2.8. 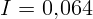 А,
А, 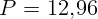 Вт.
Вт.
1.2.9. 0,7 А, 0,045 А.
1.2.10. 0,22 А.
1.2.11. 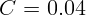 Ф.
Ф.
1.3.1. 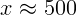 м.
м.
1.3.2. 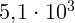 м/с,
м/с, 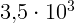 м/с,
м/с, 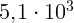 м/с.
м/с.
1.3.3. На угол, немного меньший, чем 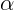 .
.
1.3.4. 3300 Гц, 330 Гц, 34 Гц.
1.3.5. 1760 Гц.
1.3.6. 1070 Гц, 940 Гц.
1.3.7. Хлопок соответствует приходу ударной волны, которая движется быстрее звуковых.
1.3.8. 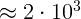 атм.
атм.
1.3.9. 8,5 Гц.
1.3.10.  Гц.
Гц.
1.4.1. 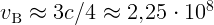 м/с,
м/с, 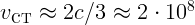 м/с.
м/с.
1.4.2. 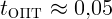 с,
с, 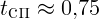 с.
с.
1.4.3.
1.4.4. 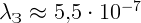 м,
м, 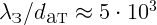 .
.
1.4.5. 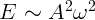 .
.
1.4.6.
1.4.7. 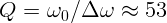 .
.
2.1.1. 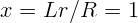 м.
м.
2.1.2. Порядка 5 м.
2.1.3. 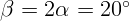 .
.
2.1.4. Половине роста человека.
2.1.5. 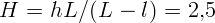 м.
м.
2.1.6. 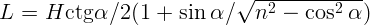 .
.
2.1.7. 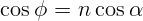 ,
, 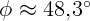 .
.
2.1.8. 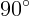 .
.
2.1.9.  .
.
2.1.10. 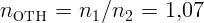 .
.
2.1.11. 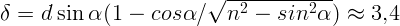 мм.
мм.
2.1.12. 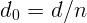 .
.
2.1.13. 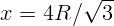 .
.
2.1.14. 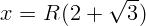 .
.
2.1.15. От центра зеркала до бесконечности.
2.1.16. 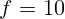 см.
см.
2.1.17. 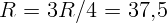 см.
см.
2.1.18. 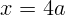 .
.
2.1.19.
2.1.20. 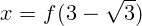 .
.
2.1.21. 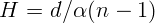 .
.
2.1.22. 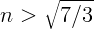 .
.
2.1.23. 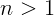 .
.
2.1.24. 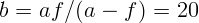 см.
см.
2.1.25. 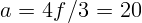 см.
см.
2.1.26. 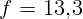 см.
см.
2.1.27. 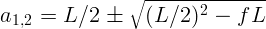 ;
; 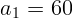 см,
см, 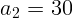 см.
см.
2.1.28. 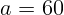 см,
см, 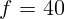 см.
см.
2.1.29. 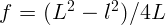 .
.
2.1.30. 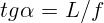 .
.
2.1.31. 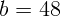 см.
см.
2.1.32.
2.1.33.
2.1.34. 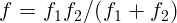 .
.
2.1.35. 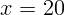 см.
см.
2.1.36. 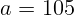 см.
см.
2.1.37. 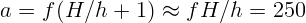 м.
м.
2.1.38. 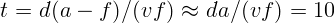 с.
с.
2.1.39. 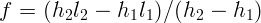 .
.
2.1.40. 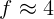 см.
см.
2.1.41. 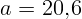 см.
см.
2.1.42. 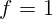 м.
м.
2.1.43. 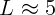 км.
км.
2.1.44. 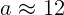 см.
см.
2.1.45. 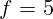 см.
см.
2.1.46. 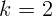 .
.
2.1.47. 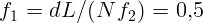 см.
см.
2.1.48. 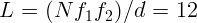 см.
см.
2.1.49. 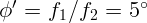 .
.
2.1.50. 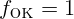 см,
см, 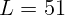 см.
см.
2.2.1. 500 с.
2.2.2. 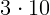 м/с.
м/с.
2.2.3. 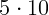 с.
с.
2.2.4. 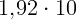 м/с.
м/с.
2.2.5. 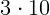 м/с.
м/с.
2.2.6. 40 полос, 5 мм.
2.2.7. 0,75 мм.
2.2.8. до 100 см, на 75 см, 0,075 мм.
2.2.9. 500 нм.
2.2.10. 12,5 см, 0, 16 мм, примерно 800 полос.
2.2.11. 0,75 мм.
2.2.12. 500 нм.
2.2.13. 10 Гц.
2.2.14. 551 нм.
2.2.15. 176 см.
2.2.16. 500 нм.
2.2.17. 10 мм.
2.2.18. порядка одного штриха на мм.
2.2.19. 400 нм.
2.2.20. примерно 2,8 мм.
2.3.1.
2.3.2. 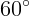 .
.
2.3.3. в два раза.
2.3.4. зеленовато-голубой.
2.3.5. белого, красно-оранжевого, желто-зеленого.
2.3.6. желто-оранжевый.
2.3.7. 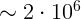 км.
км.
2.4.1. 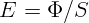 = 100 лк.
= 100 лк.
2.4.2. 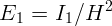 = 12,5 лк,
= 12,5 лк, 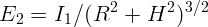 = 4,4 лк.
= 4,4 лк.
2.4.3. 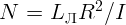 = 5 светлячков.
= 5 светлячков.
2.4.4. 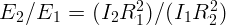 = 3.
= 3.
2.4.5. 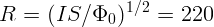 км.
км.
2.4.6. Увеличится на 0,5 лк.
2.4.7. 50 кд, в 16 раз.
2.4.8. 0,28 сб.
2.4.9. 0,075 лк.
2.4.10. 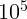 сб.
сб.
3.1.1. 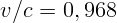 .
.
3.1.2. 0,866  .
.
3.1.3. 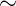 21000 МэВ.
21000 МэВ.
3.1.4. 0,866 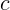 .
.
3.1.5. 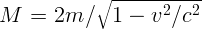 .
.
3.1.6. 2,0 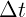 .
.
3.1.7. 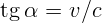 .
.
3.1.8. 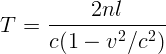 .
.
4.1.1. 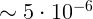 В.
В.
4.1.2. 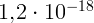 м.
м.
4.1.3. 54,5 эВ.
4.1.4. 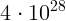 м.
м.
4.1.5. 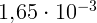 .
.
4.2.1. 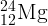 ,
, 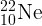 – изотоп неона.
– изотоп неона.
4.2.2. 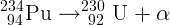 ,
, 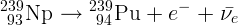 .
.
4.2.3. 21 тыс. лет.
4.2.4. увеличится в 4 раза.
4.2.5. 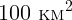
4.2.6. 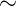 50%
50%
4.3.1. 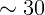 ТэВ.
ТэВ.
4.3.2. все противоречат, кроме первого распада.
4.3.3. 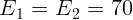 МэВ.
МэВ.
4.3.4. 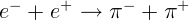 .
.